UNION AND INTERSECTION PRACTICE PROBLEMS

Question 1 :

Place the elements of the following sets in the proper location on the given Venn diagram.

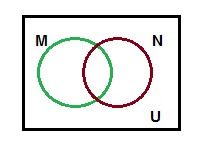
U  =  {5, 6, 7, 8, 9, 10, 11, 12, 13}

M  =  {5, 8, 10, 11}

N  =   {5, 6, 7, 9, 10}.

Solution :

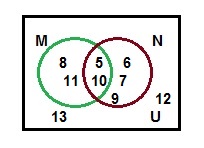
Question 2 :

If A and B are two sets such that A has 50 elements, B has 65 elements and A∪B has 100 elements, how many elements in A∩B?

Solution :

Given n(A)  =  50, n(B)  =  65, n(A∪B)  =  100

By the rule,

n(A∪B)  =  n(A) + n(B) - n(A∩B)

n(A∩B)  =  n(A) + n(B) - n(A∪B)

=  50+65-100

=  115-100

=  15

Question 3 :

If A and B are two sets containing 13 and 16 elements respectively, then find the minimum and maximum number of elements in A∪B?

Solution :

n(A)  =  13 and n(B)  =  16

n( A∪B) must be either the elements of the bigger set, that is B or the addition of number of elements in both A and B.

If A is the subset of B, then  A∪B is the set B itself. Then the number of A∪B is number of B itself. That is the minimum number of  A∪B.

So minimum of  A∪B is 16.

If A and B are two disjoint sets, then number of elements in  A∪B is the total number of elements in both A and B. 

So, the maximum of A∪B is 13+16  =  29.

Question 4 :

If n( A∩B)  =  5, n(A∪B)  =  35, n(A)  =  13, find n(B)?

Solution :

By the rule

n(A∪B) = n(A) + n(B) - n(A∩B)

n(B) = n(A∪B)+n(A∩B)-n(A)

=  35 + 5 - 13

n(B) = 27

Question 5 :

If n(A) = 26, n(B) = 10, n(A∪B) = 30, n(A') =17, find n(A∩B) and n(U)?

Solution :

n(A∪B)  =  n(A)+n(B)-n(A∩B)

n(A∩B)  =  n(A)+n(B)-n(A∪B)

n(A∩B)  =  26+10-30

n(A∩B)  =  6

n(A) + n(A')  =  n(U)

n(U)  =  26+17

n(U)  =  43

Question 6 :

If n(U) = 38, n(A) = 16,  n(A∩B) = 12, n(B') = 20, find n(A∪B)?

Solution :

n(A) + n(A') =  n(U)

n(B)  =  n(U)-n(B')

n(B)  =  38 - 20

n(B)  =  18

n(A∪B) =  n(A)+n(B)- n(A∩B)

n(A∪B)  =  16+18-12

n(A∪B)  =  34-12

n(A∪B)  =  22

Question 7 :

Let A and B be two finite sets such that n(A-B) = 30, n(A∪B) = 180, n(A∩B) = 60, find n(B)?

Solution :

n(A)  =  n(A-B) + n(AnB)

n(A)  =  30+60

n(A)  =  90

n(AuB)  =  n(A) + n(B) - n(AnB)

180  =  90 + n(B) - 60

180-30  =  n(B)

n(B)  =  150

Apart from the stuff given in this section,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.