PARTIAL FRACTIONS EXAMPLES
Partial Fractions Examples :
Here we are going to see some example problems on partial fractions.
Partial Fractions Examples
Example 1 :
Resolve into partial fractions.
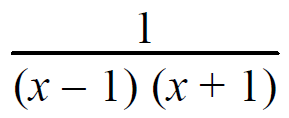
Solution :
1/(x - 1) (x + 1) = A/(x - 1) + B/(x + 1)
1/(x - 1) (x + 1) = A(x + 1) + B(x - 1)/(x - 1)(x + 1)
Since we have same denominators on both side, we can equate the numerators.
1 = A(x + 1) + B(x - 1) ------(1)
The constants A and B can also be found by successively giving suitable values for x.
To find A, put x = 1 in (1)
To find B, put x = -1 in (1)
|
1 = A(1 + 1) + B(1 - 1) 1 = 2A + B (0) 1 = 2A + 0 2A = 1 ===> A = 1/2 |
1 = A(-1 + 1) + B(-1 - 1) 1 = A(0) + B (-2) 1 = 0 - 2B -2B = 1 ===> B = -1/2 |
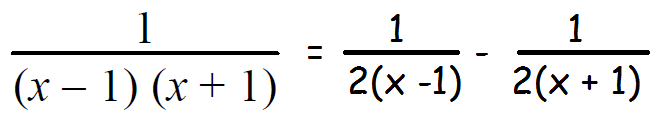
Example 2 :
Resolve into partial fractions.
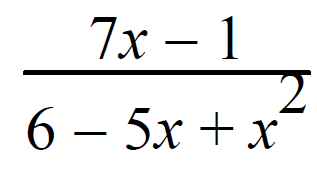
Solution :
7x - 1/(x2-5x + 6) = 7x - 1/(x - 3) (x - 2)
7x - 1/(x - 3) (x - 2) = A/(x - 3) + B/(x - 2)
7x - 1/(x - 3) (x - 2) = A(x - 2) + B(x - 3)/(x - 3)(x - 2)
Since we have same denominators on both side, we can equate the numerators.
7x - 1 = A(x - 2) + B(x - 3) ------(1)
The constants A and B can also be found by successively giving suitable values for x.
To find A, put x = 3 in (1)
To find B, put x = 2 in (1)
|
7(3) - 1 = A(3-2)+B(3-3) 21 - 1 = 1A + B (0) 20 = A + 0 A = 20 |
7(2) - 1 = A(2-2)+B(2-3) 14 - 1 = A(0) + B (-1) 13 = 0 - B B = -13 |
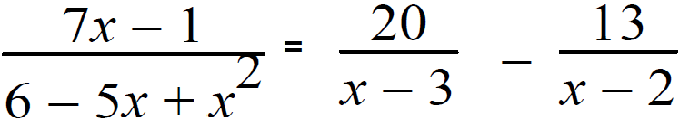
Example 3 :
Resolve into partial fractions.
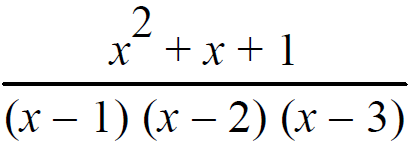
Solution :
(x2+ x + 1)/(x-1)(x-2)(x-3) = A/(x-1) + B/(x-2) + C/(x-3)
Taking L.C.M
= A(x-2)(x-3) + B(x-1)(x-3) + C(x-2)(x-1)/(x-1)(x-2)(x-3)
Since we have same denominators on both side, we can equate the numerators.
x2+ x + 1 = A(x-2)(x-3) + B(x-1)(x-3) + C(x-2)(x-1) ----(1)
The constants A, B and C can also be found by successively giving suitable values for x.
To find A, put x = 1 in (1)
To find B, put x = 2 in (1)
To find C, put x = 3 in (1)
|
If we put x = 1, both B and C will become zero. |
12+ 1 + 1 = A(1-2)(1-3) 3 = A(-1)(-2) 2A = 3 ==> A = 3/2 | |
|
If we put x = 2, both A and C will become zero. |
22+ 2 + 1 = B(2-1)(2-3) 4 + 2 +1 = B(1)(-1) 7= -B ==> B = -7 | |
|
If we put x = 3, both C and B will become zero. |
32+ 3 + 1 = C(3-2)(3-1) 9 + 3 + 1 = C(1)(2) 13 = 2C ==> C = 13/2 |
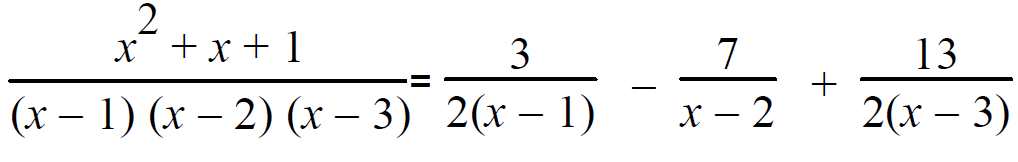
Example 4 :
Resolve into partial fractions.
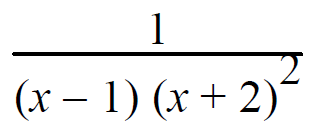
Solution :
1/(x-1)(x+2)2 = A/(x-1) + B/(x+2) + C/(x+2)2
Taking L.C.M
1/(x-1)(x+2)2 = A(x+2)2 + B(x-1)(x+2) + C(x-1)/(x-1)(x+2)2
Since we have same denominators on both side, we can equate the numerators.
1 = A(x+2)2 + B(x-1)(x+2) + C(x-1) ----(1)
By equating the coefficients of x2, x and constant terms respectively, we get
A + B = 0 -------(2)
4A + B + C = 0 -------(3)
4A - 2B - C = 1 -------(4)
By adding the equations (3) and (4) we get,
00000000000004A + B + C = 000000000000000000000
00000000000004A - 2B - C = 10000000000000000000
000000000000-------------------0000000000000000000
0000000000008A - B = 1------(5)00000000000000000
(5) + (2)
A + B + 8A - B = 0 + 1
9A = 1 ==> A = 1/9
|
Substituting the value of A in (2), we get 1/9 + B = 0 B = -1/9 |
Substituting the values of A and B in (3), we get 4(1/9) + (-1/9) + C = 0 4/9 - 1/9 + C = 0 (4 - 1 + 9C)/9 = 0 3 + 9C = 0 9C = -3 C = -3/9 ==> -1/3 |
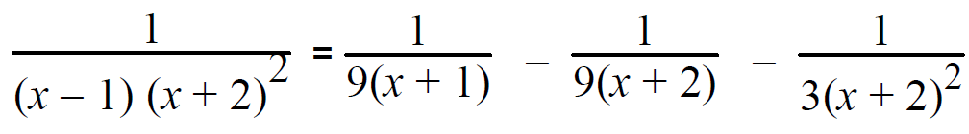
Example 5 :
Resolve into partial fractions.
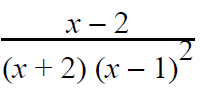
Solution :
(x - 2)/(x+2)(x-1)2 = A/(x + 2) + B/(x - 1) + C/(x - 1)2
Taking L.C.M
(x-2)/(x+2)(x-1)2 = A(x-1)2+B(x-1)(x+2)+C(x+2)/(x+2)(x-1)2
Since we have same denominators on both side, we can equate the numerators.
x - 2 = A(x - 1)2 + B(x - 1)(x + 2) + C(x + 2) --(1)
By equating the coefficients of x2, x and constant terms respectively, we get
A + B = 0 -------(2)
-2A + B + C = 1 -------(3)
A - 2B + 2C = -2 -------(4)
2 x (3) - (4)
2(-2A + B + C) - (A - 2B + 2C) = 2 - (-2)
-4A - A + 2B + 2B + 2C - 2C = 2 + 2
-5A + 4B = 4 -------(5)
5 x (2) + (5)
5A + 5B + (-5A + 4B) = 0 + 4
5A + 5B -5A + 4B = 4
9B = 4 ==> B = 4/9
|
Substituting the value of B in (2), we get A + 4/9 = 0 A = -4/9 |
Substituting the values of A and B in (3), we get -2(-4/9) + 4/9 + C = 1 8/9 + 4/9 + C = 1 (8 + 4 + 9C)/9 = 1 12 + 9C = 9 9C = -3 C = -1/3 |
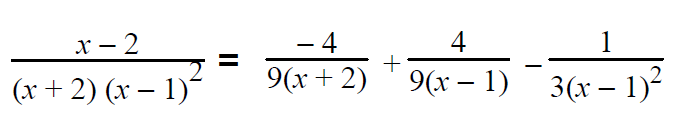

After having gone through the stuff given above, we hope that the students would have understood, how to decompose a rational expression into partial fractions.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number