COMPARING AND ORDERING WHOLE NUMBERS
The set of all non negative integers is whole numbers.
That is,
W = {0, 1, 2, 3, 4, .......}
We use number line to compare and order whole numbers.
That is, if we want to compare two whole numbers, first we have to locate the numbers on the number line and mark them.
The number which comes to the right of the other number is greater. The number which comes to the left of the other number is smaller.
To order the whole numbers, we have to locate the given numbers on the number line and mark them. Then, write the numbers from left to right to list them in order from least to greatest.
Comparing Whole Numbers
Example 1 :
Compare the whole numbers 3 and 6.
Solution :
Let us locate the two whole numbers 3 and 6 on a number line and mark them.

Here, 6 comes to the right of 3.
Therefore 6 is greater than 3.
And 3 comes to the left of 6.
Therefore 3 is smaller than 6.
Example 2 :
Compare the whole numbers 6 and 9.
Solution :
Let us locate the two whole numbers 6 and 9 on a number line and mark them.
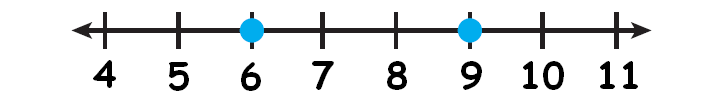
Here, 9 comes to the right of 6.
Therefore 9 is greater than 6.
And 6 comes to the left of 9.
Therefore 6 is smaller than 9.
Ordering Whole Numbers
Question :
Order the whole numbers 12, 5, 9, 6, 1, 3 from least to greatest.
Solution :
Let us locate the whole numbers 12, 5, 9, 6, 1, 3 on a number line and mark them.

From the above number line, write the whole numbers from left to right to list them in order from least to greatest.
Thus, we get
1, 3, 5, 6, 9, 12
Real World Problems
Problem 1 :
In 2010, Sacramento, California, received 23 inches in annual precipitation. In 2011, the city received 17 inches in annual precipitation. In which year was there more precipitation ?
Solution :
Locate the two whole numbers 23 and 17 on a number line and mark them.
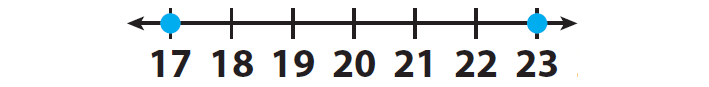
23 is to the right of 17 on the number line.
This means that 23 is greater than 17.
We can write the above situation in terms of inequality as 23 > 17.
17 is to the left of 23 on the number line.
This means that 17 is less than 23.
We can write the above situation in terms of inequality as 17 < 23.
There was more precipitation in 2010.
Problem 2 :
John recorded the following golf scores during his first week at a golf academy. In golf, a lower score beats a higher score.
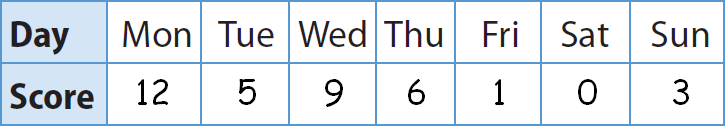
Graph John’s scores on the number line, and then list the numbers in order from least to greatest.
Solution :
Step 1 :
Graph the scores on the number line.

Step 2 :
Read from left to right to list the scores in order from least to greatest.
The scores listed from least to greatest are
0, 1, 3, 5, 6, 9, 12
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane