NCERT solutions for class 10 maths chapter 3 part 5

In this page NCERT solutions for class 10 maths chapter 3 part 5 you can find solutions for exercise problems.

NCERT solutions for class 10 maths chapter 3 part 5

(5) Half the perimeter of a rectangular garden,whose length is 4 m more its width,is 36 m. Find the dimensions of the garden.

Solution:

Let "x" be the width of the rectangular garden

Let "y" be its length

y = x + 4  -------- (1)

Half the perimeter of the rectangular garden = 36 m

perimeter of rectangle = 2 (L + b)

L + b = 36

y + x = 36

y = 36 - x -------- (2)

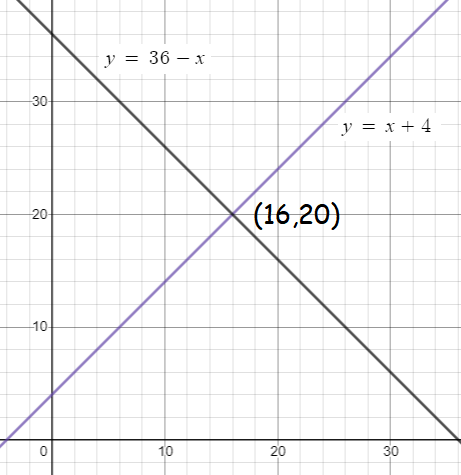
The point of intersection of those two lines is (16,20). So,length of the rectangular garden is 20 m and width of the rectangular garden is 16 m.

(6) Given the linear equation 2 x + 3 y - 8 = 0,write another linear equation in two variables such that the geometrical representation of the pair so formed is:

Solution:

(i) intersecting lines

The condition for intersection of two lines is a₁/a₂ ≠ b₁/b₂.According to the above condition,we have to form a equation.

 a₁ = 2          b₁ = 3            c₁ = -8

The values of a₂,b₂ and c₂ be any real values but the simplified values of a₁/a₂ and b₁/b₂ shouldn't be equal.

 a₂ = 3         b₂ = -3            c₂ = -16

So one of the possible required equation is 3 x - 3 y - 16 = 0.

(ii) Parallel lines

The condition  for two parallel lines is a₁/a₂ = b₁/b₂ ≠ c₁/c₂.According to the above condition,we have to form a equation.

 a₁ = 2          b₁ = 3            c₁ = -8

if the value of a₂ is 4,the value of b₂ will be 6. The value of c₂ must be any value other than -16.

 a₂ = 4         b₂ = 6            c₂ = 6

So one of the possible required equation is 4 x + 6 y - 6 = 0.

(iii) Coincident lines

The condition  for coincident lines is a₁/a₂ = b₁/b₂ = c₁/c₂.According to the above condition,we have to form a equation.

 a₁ = 2          b₁ = 3            c₁ = -8

the values of a₂,b₂ and c₂ will be

 a₂ = 4         b₂ = 6            c₂ = -16

So one of the possible required equation is 4 x + 6 y - 16 = 0.

(7) Draw the graphs of the equations x - y + 1 = 0 and 3 x + 2 y - 12 = 0. Determine the coordinates of the vertices of the triangle formed be these lines and the x-axis and shade the triangular region.




HTML Comment Box is loading comments...