HOW TO FIND THE SLOPE OF ALTITUDE OF A TRIANGLE
In the Δ ABC shown below,
AD ⊥ BC, BE ⊥ AC, CF ⊥ AB
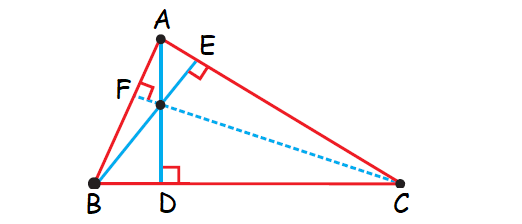
The line segments AD, BE and CF are called altitudes of the triangle ABC.
Since AD ⊥ BC, product of slopes of AD and BC is equal to -1.
slope of AD x slope of BC = -1
slope of AD = -1/slope of BC
Similarly,
slope of BE = -1/slope of AC
slope of CF = -1/slope of AB
Example :
Let A(1, 2), B(-4, 5) and C(0, 1) be the vertices of the Δ ABC. Find the slopes of the altitudes AD, BE and CF.
Solution :
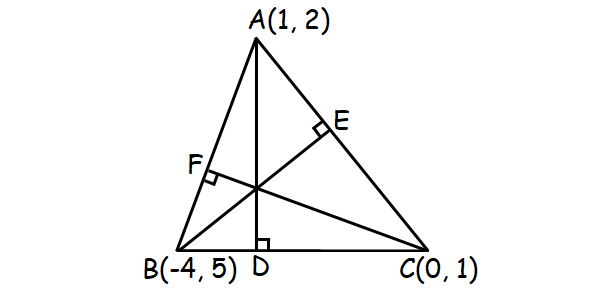
Slope of AD :
Use slope formula and find the slope of BC.
m = (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = B(-4, 5) and (x2, y2) = C(0, 1).
slope of BC = (1 - 5)/(0 + 4)
= -4/4
= -1
slope of AD = -1/slope of BC
= -1/(-1)
= 1
Slope of BE :
m = (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(1, 2) and (x2, y2) = C(0, 1).
slope of AC = (1 - 2)/(0 - 1)
= -1/(-1)
= 1
slope of BE = -1/slope of AC
= -1/1
= -1
Slope of CF :
m = (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(1, 2) and (x2, y2) = B(-4, 5).
slope of AB = (5 - 2)/(-4 - 1)
= 3/(-5)
= -3/5
slope of CF = -1/slope of AB
= -1/(-3/5)
= 5/3
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
