ANGLE BETWEEN TWO STRAIGHT LINES
Two straight lines in a plane would either be parallel or coincide or intersect. Normally when two straight lines intersect, they form two angles at the point of intersection. One is an acute angle and another is an obtuse angle or equal. Both these angles would be supplements (Sum equals 180°) of each other. By definition, when we say ‘angle between two straight lines’ we mean the acute angle between the two lines.
Let y = m1x + c1 and y = m2x + c2. be the equations of two straight lines and let these two lines make angles A and B with x- axis.
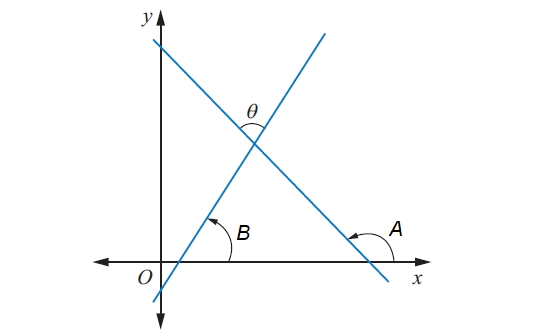
Then, m1 = tanA and m2 = tanB.
If θ is the angle between two straight lines, then
θ = A - B
tanθ = tan(A - B)
tanθ = (tanA - tanB)/(1 + tanAtanB)
θ = (m1 - m2)/(1 + m1m2)
θ = tan-1[(m1 - m2)/(1 + m1m2)]
If (m1 - m2)/(1 + m1m2) is positive, then θis the acute angle and if it is negative θ is the obtuse angle between the two lines. Therefore the acute angle θ is
tan-1|(m1 - m2)/(1 + m1m2)|
Example 1 :
Find the angle between the straight lines :
3x - 2y + 9 = 0
2x + y - 9 = 0
Solution :
Write each equation in slope intercept form.
|
3x - 2y + 9 = 0 -2y = -3x - 9 y = (3/2)x + 9/2 slope = 3/2 |
2x + y - 9 = 0 y = -2x + 9 slope = -2 |
Formula to find angle between the two straight lines :
θ = tan-1|(m1 - m2)/(1 + m1m2)|
Substitute m1 = 3/2 and m2 = -2.
= tan-1|(3/2 - 2)/(1 + (3/2)(-2))|
= tan-1|(3/2) + 2))/(1 - 3)|
= tan-1|(7/2)/(- 2)|
= tan-1|-7/4|
= tan-1(7/4)
Example 2 :
Show that the following two straight lines are parallel.
2x + y - 9 = 0
2x + y - 10 = 0
Solution :
Write each equation in slope intercept form.
|
2x + y - 9 = 0 y = -2x + 9 slope = -2 |
2x + y - 10 = 0 y = -2x + 10 slope = -2 |
Formula to find angle between the two straight lines :
θ = tan-1|(m1 - m2)/(1 + m1m2)|
Substitute m1 = -2 and m2 = -2.
= tan-1|(-2 + 2)/(1 + (-2)(-2))|
= tan-1|0/(1 + 4)|
= tan-1|0|
= 0°
Since the angle between the given two straight lines is 0°, the lines are parallel.
Example 3 :
Show that the following two straight lines are perpendicular.
2x + 3y - 9 = 0
3x - 2y + 10 = 0
Solution :
Write each equation in slope intercept form.
|
2x + 3y - 9 = 0 3y = -2x + 9 y = (-2/3)x + 3 slope = -2/3 |
3x - 2y + 10 = 0 -2y = -3x - 10 y = (3/2)x + 5 slope = 3/2 |
Formula to find angle between the two straight lines :
θ = tan-1|(m1 - m2)/(1 + m1m2)|
Substitute m1 = -2/3 and m2 = 3/2.
= tan-1|(-2/3 + 3/2)/(1 + (-2/3)(3/2))|
= tan-1|(5/9)/(1 - 1)|
= tan-1|(5/9)/0|
= tan-1(∞)
= 90°
Since the angle between the given two straight lines is 90°, the lines are parallel.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
