FIND THE MISSING EXPONENT

The exponent of a number says how many the number has to be multiplied by itself.

In 9² the '2' says that 9 has to be used twice twice in multiplication, so 9² = 9 × 9 = 81.

In words : 9² can be called '9 to the power 2' or '9' to the second power, or simply '9 squared' Exponents are also called Powers or Indices.

We can follow the steps given below to find the missing exponent. 

Step 1 :

To find the missing exponent, we have to get the same base on both sides. 

Step 2 :

Once we get the same base, exponents can be equated and we can find the value of the missing exponent.  

Examples

Example 1 :

Find the missing exponent.

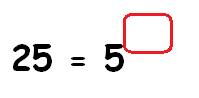
Solution :

Let 'x' be the missing exponent. 

Then, 

25  =  5^x

To get the same base on both sides, write 25 in terms of 5 using exponent. 

5²  =  5^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 2 :

Find the missing exponent.

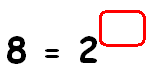
Solution :

Let 'x' be the missing exponent. 

Then, 

8  =  2^x

To get the same base on both sides, write 8 in terms of 2 using exponent. 

2³  =  2^x

Equate the exponents. 

3  =  x

So, the missing exponent is 3.

Example 3 :

Find the missing exponent.

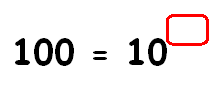
Solution :

Let 'x' be the missing exponent. 

Then, 

100  =  10^x

To get the same base on both sides, write 100 in terms of 10 using exponent. 

10²  =  10^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 4 :

Find the missing exponent.

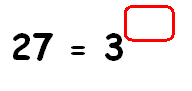
Solution :

Let 'x' be the missing exponent. 

Then, 

27  =  3^x

To get the same base on both sides, write 27 in terms of 3 using exponent. 

3³  =  3^x

Equate the exponents. 

3  =  x

So, the missing exponent is 3.

Example 5 :

Find the missing exponent.

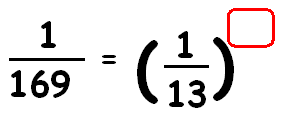
Solution :

Let 'x' be the missing exponent. 

Then, 

1/169  =  (1/13)^x

Write 169 in terms of 13 using exponent. 

1/13²  =  (1/13)^x

13^-2  =  (13^-1)^x

13^-2  =  13^-x

Equate the exponents. 

-2  =  -x

Multiply each side by (-1).

2  =  x

So, the missing exponent is 2.

Example 6 :

Find the missing exponent.

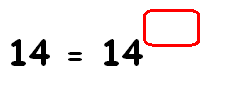
Solution :

Let 'x' be the missing exponent. 

Then, 

14  =  14^x

Already, we have the same on both sides.

14¹  =  14^x

Equate the exponents. 

1  =  x

So, the missing exponent is 1.

Example 7 :

Find the missing exponent.

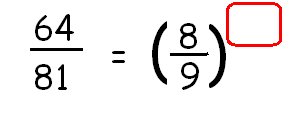
Solution :

Let 'x' be the missing exponent. 

Then, 

64/81  =  (8/9)^x

Write 64 in terms 8 and 81 in terms of 9 using exponent. 

8² / 9²  =  (8/9)^x

(8/ 9)²  =  (8/9)^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 8 :

Find the missing exponent.

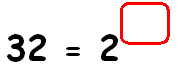
Solution :

Let 'x' be the missing exponent. 

Then, 

32  =  2^x

Write 32 in terms of 2 using exponent. 

2⁵  =  2^x

Equate the exponents. 

5  =  x

So, the missing exponent is 5.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.