OPERATIONS WITH RATIONAL NUMBERS PROBLEMS 

Problem 1 :

Fill in the blanks

(i)  The multiplicative inverse of 2  3/5 is  _______

Solution :

For any non-zero rational number b there exists a unique rational number 1/b such that b x (1/b) =  1  =  (1/b) × b (Multiplicative Inverse property).

First let us convert the mixed fraction into improper fraction.

2  3/5  =  (10 + 3)/5  =  13/5

The multiplicative inverse of 13/5 is 5/13.

(ii) If −3 ⋅ (6/-11)  =  (6/-11) ⋅ x, then x is ________.

Solution :

In order to get same answer for both left hand side and right hand side, we have to remember the commutative law.

a x b  =  b x a

So, the value of x is -3.

(iii) If distributive property is true for

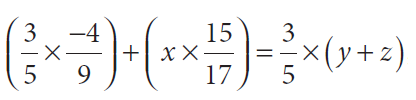
then x, y, z are ________ , ________ and ________.

Solution :

R.H.S :

  =  (3/5) (y + z)

  =  (3/5) ⋅ y + (3/5) ⋅ z   ------(1)

L.H.S :

(3/5) ⋅ (-4/9) + (x ⋅ (15/17))   ------(2)

(1)  =  (2)

 (3/5) ⋅ (-4/9) + (x ⋅ (15/17))  =  (3/5) ⋅ y + (3/5) ⋅ z  

x  =  3/5, y  =  -4/9 and z  =  15/17

(iv) If x ⋅ (-55/63)  =  (-55/63) ⋅  x  =  1, then x is called the _________________ of 55/63 . 

Solution :

Since the product of x and -55/63 is 1, we say that x is the multiplicative inverse of -55/63.

Hence the value of x is -63/55.

(v) The multiplicative inverse of -1 is ________.

Solution :

The multiplicative inverse of -1 is -1.

Problem 2 :

Say True or False:

(i)  (−7/8) × (−23/27)  = (−23/27) × (−7/8) illustrates the closure property of rational numbers.

Solution :

The given statement exactly matches with the general form

 a x b  =  b x a

It means commutative property not closure.

Hence the answer is False.

(ii)  Associative property is not true for subtraction of rational numbers.

Solution :

(a - b) - c  =  a - (b - c)

If associative property is true, then it satisfies the above statement.

Let a = 1/2, b = 1/3 and c = 5/6

(a - b) - c  =  [(1/2) - (1/3)] - 5/6

  =  (1/6) - (5/6)

  =  (1-5)/6

  =  -4/6

  =  -2/3 -----(1)

a - (b - c)  =  (1/2) - [(1/3)- 5/6]

  =  (1/2) - (-3/6)

  =  (3 + 3)/6

  =  1 -----(2)

Hence the answer is True.

(iii)  The additive inverse of −11/(-17) is 11/17.

Solution :

The answer is false.

By simplifying 11/17 and 11/17, we will not get 0.

(iv) The product of two negative rational numbers is a positive rational number

Solution :

The answer is True. Because negative times negative is positive.

(v) The multiplicative inverse exists for all rational numbers.

Solution :

For the rational number 0 there is no multiplicative inverse. Hence the answer is false.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.