SOLVING SYSTEM OF EQUATIONS WITH FRACTIONS BY ELIMINATION
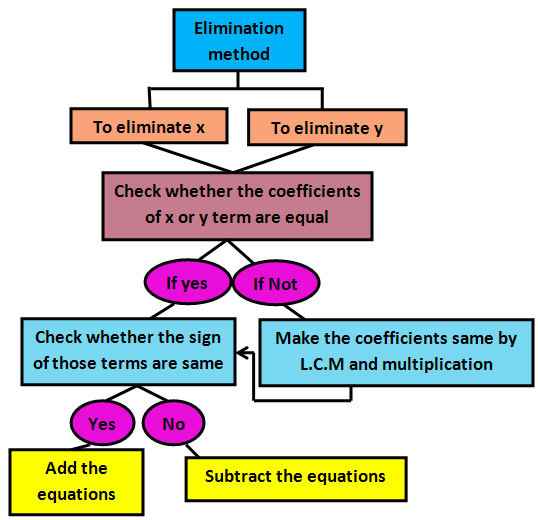
The flow chart shown below explains the steps to be done in solving system of linear equations with two unknowns 'x' and 'y' using elimination method.
Solved Examples
Question 1 :
Solve the following system of linear equations by elimination method.
15/x + 2/y = 17
1/x + 1/y = 36/5
Solution :
Let a = 1/x and b = 1/y.
Then,
15a + 2b = 17 -----(1)
a + b = 36/5 -----(2)
(1) - 2(2) :
13a = 17 - 72/5
13a = (85 - 72) / 5
13a = 13/5
Divide each side by 13.
a = 1/5 -----(3)
Substitute 1/5 for a in (1).
(1)-----> 15(1/5) + 2b = 17
3 + 2b = 17
Subtract 3 from each side.
2b = 14
Divide each side by 2.
b = 7 ----->(4)
In (3) and (4), substitute 1/x for 'a' and 1/y for b.
|
1/x = 1/5 x = 5 |
1/y = 7 y = 1/7 |
Question 2 :
Solve the following system of linear equations by elimination method
2/x + 2/3y = 1/6
3/x + 2/y = 0
Solution :
Let a = 1/x and b = 1/y.
Then,
2a + 2b/3 = 1/6 -----(1)
3a + 2b = 0 -----(2)
3(1) - (2) :
3a = 1/2
Divide each side by 3.
a = 1/6 -----(3)
Substitute 1/6 for a in (2).
(2)-----> 3(1/6) + 2b = 0
1/2 + 2b = 0
Subtract 1/2 from each side.
2b = -1/2
Divide each side by 2.
b = -1/4 -----(4)
In (3) and (4), substitute 1/x for 'a' and 1/y for b.
|
1/x = 1/6 x = 6 |
1/y = -1/4 y = -4 |

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
