DIVIDING POLYNOMIALS USING LONG DIVISION
The division of polynomials p(x) and g(x) is expressed by the following “division algorithm” of algebra.
Let p(x) and g(x) be two polynomials such that degree of p(x) ≥ degree of g(x) and g(x) ≠ 0. Then there exists unique polynomials q(x) and r (x)
such that
p(x) = g(x) q(x) + r (x) ... (1)
where r (x) = 0 or degree of r (x) < degree of g(x) .
The polynomial p(x) is the dividend, g(x) is the divisor, q(x) is the quotient and r (x) is the remainder.
(1) ==> Dividend = (Divisor x Quotient) + Remainder
Example 1 :
Divide the polynomial 2x3 - 6x2 + 5x + 4 by (x - 2)
Solution :
Let P(x) = 2x3 - 6x2 + 5x + 4 and g(x) = x - 2
To divide the given polynomial by x - 2, we have divide the first term of the polynomial P(x) by the first term of the polynomial g(x).
If we divide 2x3 by x, we get 2x2. Now we have to multiply this 2x2 by x - 2. From this we get 2x3 - 4x2.
Now we have to subtract 2x3 - 4x2 from the given polynomial. So we get -2x2 + 5x + 4.
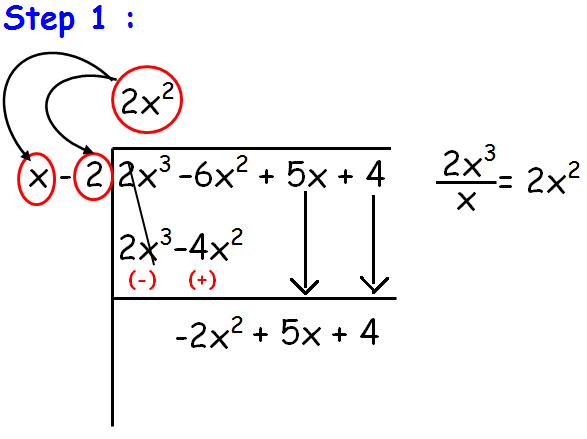
Now we have to subtract 2x3 - 4x2 from the given polynomial. So we get -2x2 + 5x + 4.
repeat this process until we get the degree of p(x) ≥ degree of g(x).
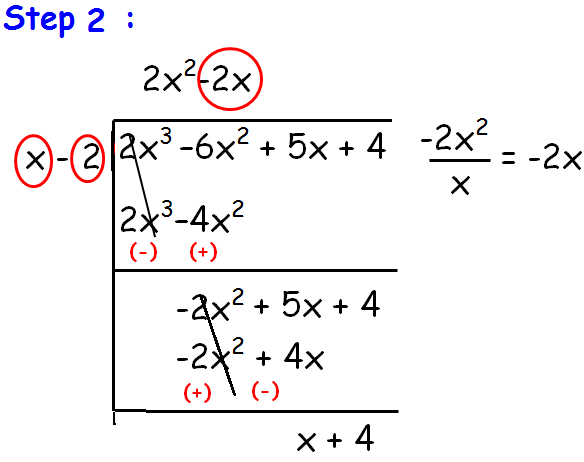
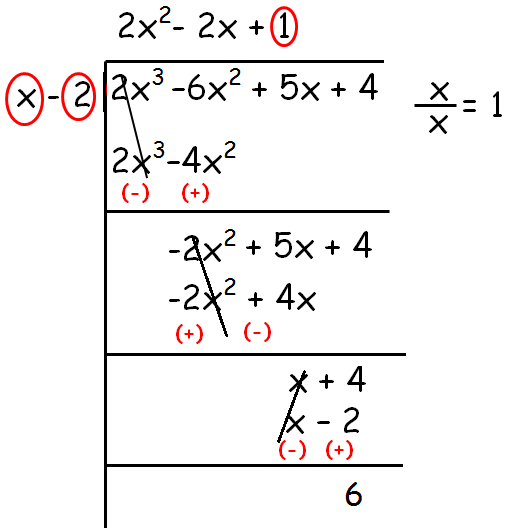
So,
Quotient = 2x2 - 2x + 1
Remainder = 6
Example 2 :
Find the quotient and remainder when 4x3 - 5x2 + 6x - 2 by x - 1.
Solution :
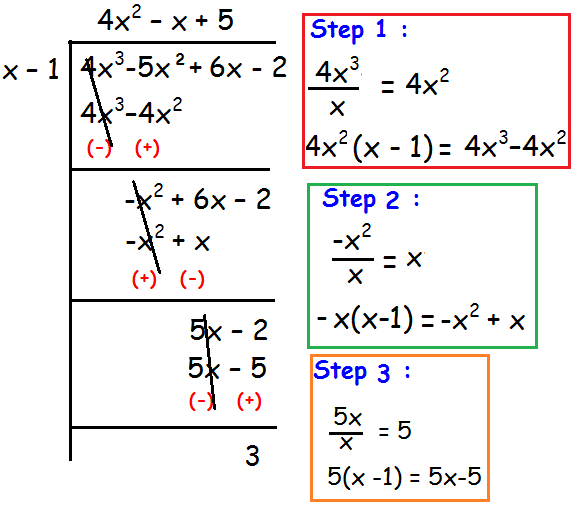
So,
Quotient = 4x2 - x + 5
Remainder = 3
Example 3 :
Find the quotient and remainder when x3 - 7x2 - x + 6 by x + 2.
Solution :
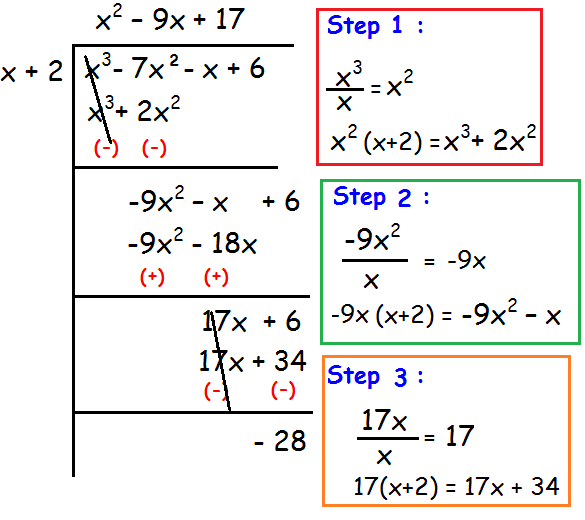
So,
Quotient = x2 - 9x + 17
Remainder = -28
Example 4 :
Find the quotient and the remainder when 10- 4x + 3x2 is divided by x - 2.
Solution :
Let us first write the terms of each polynomial in descending order ( or ascending order).
Thus, the given problem becomes (10- 4x + 3x2) ÷ (x - 2)
f(x) = 10- 4x + 3x2
= 3x2 - 4x + 10
g(x) = x - 2
Step 1 :
In the first step, we are going to divide the first term of the dividend by the first first term of the divisor.
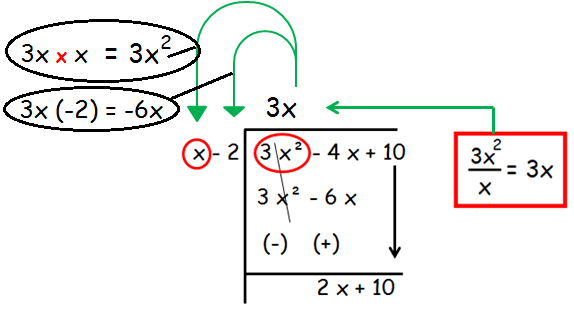
After changing the signs, +3x2 and -3x2 will get canceled. By simplifying, we get 2x + 10.
Step 2 :
In the second step again we are going to divide the first term that is 2x by the first term of divisor that is x.
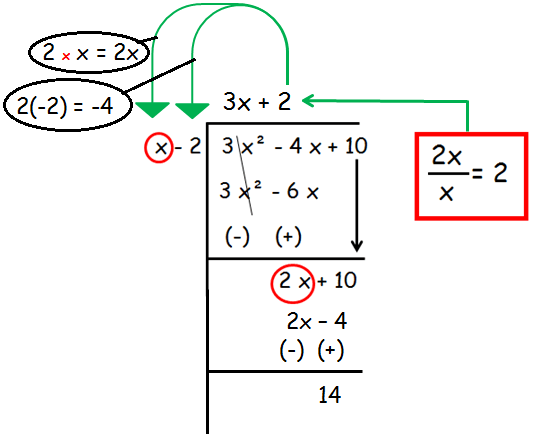
So,
Quotient = 3x + 2
Remainder = 14
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number

