CONDITION FOR PARALLEL LINES
(i) Condition for the lines to be parallel in terms of their slopes.
Let m1 and m2 be the slopes of two lines.
If the two lines are parallel, then their slopes will be equal.
That is,
m1 = m2
(ii) Condition for the lines to be parallel in terms of their general form of equations.
Let us consider the general form of equation of a straight line.
ax + by + c = 0
If the two lines are parallel, then their general forms of equations will differ only in the constant term and they will have the same coefficients of x and y.
That is,
ax + by + c1 = 0
ax + by + c2 = 0
(iii) Condition for the lines to be parallel in terms of their slope-intercept form of equations.
Let us consider the slope intercept form of equation of a straight line.
y = mx + b
If the two lines are parallel, then their slope-intercept form equations will will differ only in the "y"- intercept.
That is,
y = mx + b1
y = mx + b2
(iv) Condition for the lines to be parallel in terms of angle of inclination.
Let l1 and l2 be two lines.
If the two lines are parallel, the angle between them and the positive side of x-axis will be equal.
The figure given below illustrates the above situation.
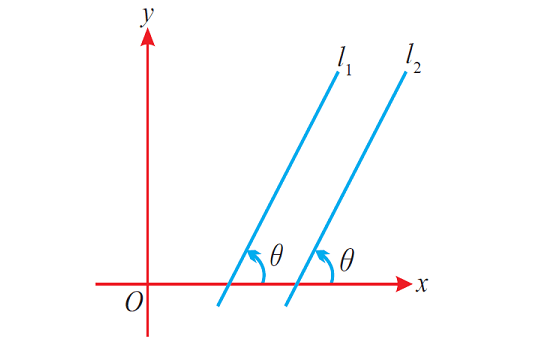
(v) Condition for the lines to be parallel in terms of the perpendicular distance between them.
If the two lines are parallel, the perpendicular distance between them will be same at everywhere.
The figure shown below below illustrates the above situation.
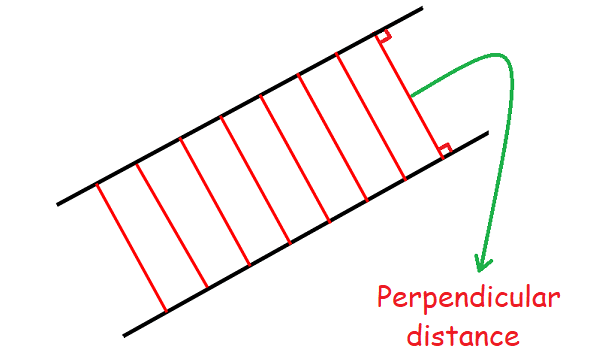
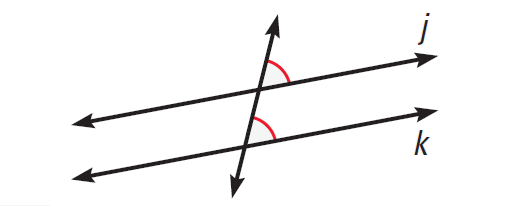
(v) Condition for the lines to be parallel when they are cut by a transversal.
Corresponding Angles Converse :
If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.
The diagram shown below illustrates this.
Alternate Interior Angles Converse :
If two lines are cut by a transversal so that alternate interior angles are congruent, then the lines are parallel.
The diagram shown below illustrates this.
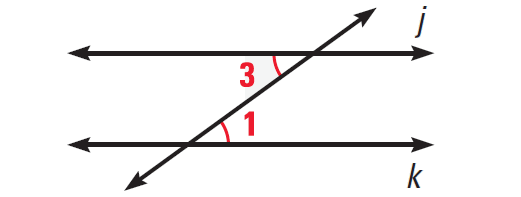
Consecutive Interior Angles Converse :
If two lines are cut by a transversal so that consecutive interior angles are supplementary, then the lines are parallel.
The diagram given below illustrates this.
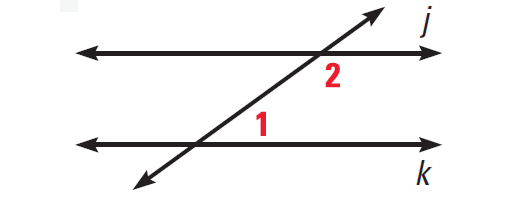
Alternate Exterior Angles Converse :
If two lines are cut by a transversal so that alternate exterior angles are congruent, then the lines are parallel.
The diagram given below illustrates this.
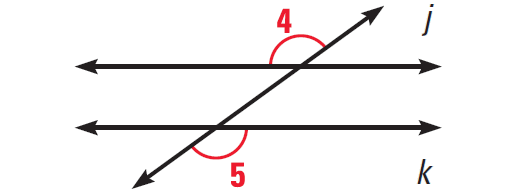
Solved Problems
Problem 1 :
The slopes of the two lines are 7 and (3k + 2). If the two lines are parallel, find the value of k.
Solution :
If two lines are parallel, then their slopes are equal.
3k + 2 = 7
Subtract 2 from each side.
3k = 5
Divide each side by 5.
k = 5/3
Problem 2 :
If the following equations of two lines are parallel, then find the value of k.
3x + 2y - 8 = 0
(5k + 3)x + 2y + 1 = 0
Solution :
If the two lines are parallel, then their general forms of equations will differ only in the constant term and they will have the same coefficients of x and y.
To find the value of k, equate the coefficients of x.
5k + 3 = 3
Subtract 3 from each side.
5k = 0
Divide each side by 5.
k = 0
Problem 3 :
Find the equation of a straight line is passing through (2, 3) and parallel to the line 2x - y + 7 = 0.
Solution :
Because the required line is parallel to 2x - y + 7 = 0, the equation of the required line and the equation of the given line 2x - y + 7 = 0 will differ only in the constant term.
Then, the equation of the required line is
2x - y + k = 0 -----(1)
The required line is passing through (2, 3).
Substitute x = 2 and y = 3 in (1).
2(2) - 3 + k = 0
4 - 3 + k = 0
1 + k = 0
k = - 1
So, the equation of the required line is
(1)-----> 2x -y - 1 = 0
Problem 4 :
Verify, whether the following equations of two lines are parallel.
3x + 2y - 7 = 0
y = -1.5x + 4
Solution :
In the equations of the given two lines, the equation of the second line is not in general form.
Let us write the equation of the second line in general form.
y = -1.5x + 4
1.5x + y - 4 = 0
Multiply by 2 on both sides,
3x + 2y - 8 = 0
Now, let us compare the equations of two lines,
3x + 2y - 7 = 0
3x + 2y - 8 = 0
The above two equations differ only in the constant term.
So, the equations of the given two lines are parallel.
Problem 5 :
Verify, whether the following equations of two lines are parallel.
5x + 7y - 1 = 0
10x + 14y + 5 = 0
Solution :
In the equation of the second line 10x + 14y + 5 = 0, the coefficients of x and y have the common divisor 2.
So, divide the second equation by 2
(10x/2) + (14y/2) + (5/2) = (0/2)
5x + 7y + 2.5 = 0
Now, let us compare the equations of two lines,
5x + 7y - 1 = 0
5x + 7y + 2.5 = 0
The above two equations differ only in the constant term.
So, the equations of the given two lines are parallel.
Problem 6 :
In the diagram given below, if ∠1 ≅ ∠2, then prove m||n.
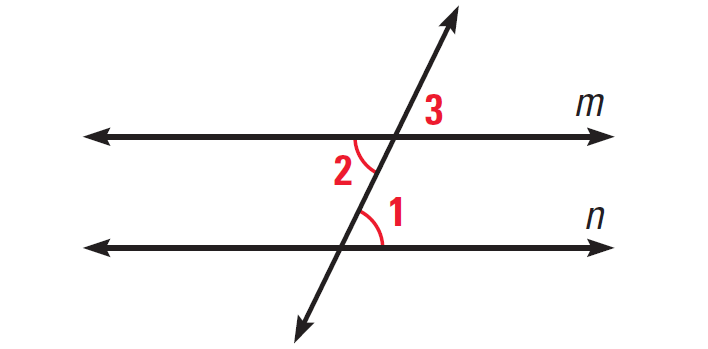
Solution :
|
Statements ∠1 ≅ ∠2 ∠2 ≅ ∠3 ∠1 ≅ ∠3 m||n |
Reasons Given Vertical angles theorem Transitive property of congruence Corresponding angles converse |
Problem 7 :
In the diagram given below, find the value of x that makes j||k.
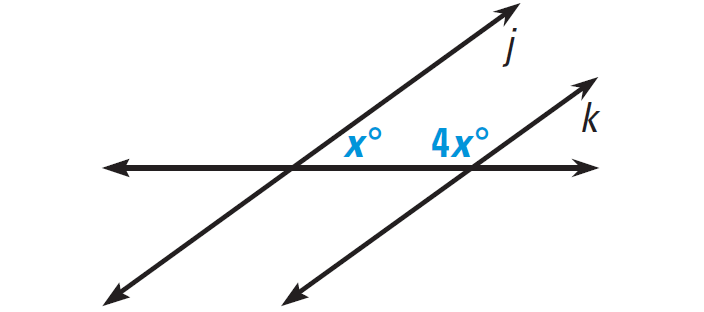
Solution :
Lines j and k will be parallel if the marked angles are supplementary.
x° + 4x° = 180°
5x = 180
x = 36
So, x = 36 makes j||k.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
