FINDING AREA OF A TRIANGLE USING COORDINATES
In Geometry, a triangle is the 3 – sided polygon which has 3 edges and 3 vertices.
Area of the triangle is a measure of the space covered by the triangle in the two-dimensional plane.
In this article, you will learn how to find the area of a triangle in the coordinate geometry.
Finding Area of a Triangle Using Coordinates :
When we have vertices of the triangle and we need to find the area of the triangle, we can use the following steps.
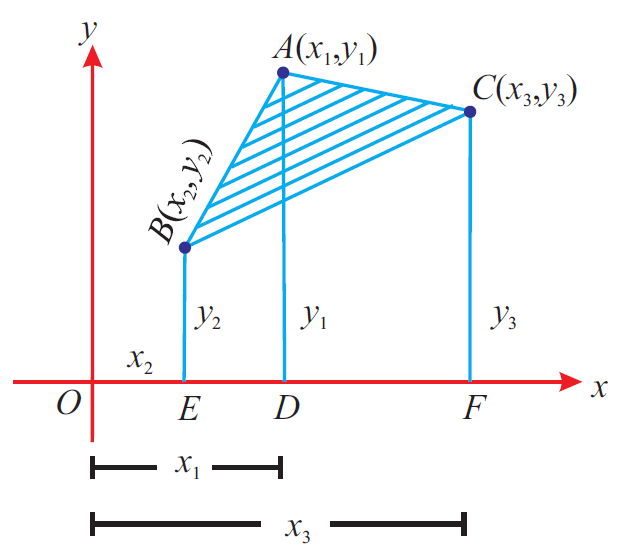
(i) Plot the points in a rough diagram.
(ii) Take the vertices in counter clock-wise direction. Otherwise the formula gives a negative value.
(iii) Use the formula given below
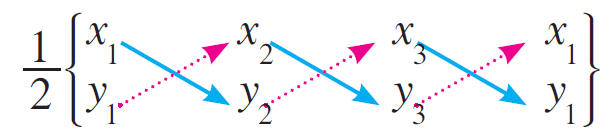
And the diagonal products x1y2, x2y3 and x3y1 as shown in the dark arrows.
Also add the diagonal products x2y1, x3y2 and x1y3 as shown in the dotted arrows.
Now, subtract the latter product from the former product to get area of the triangle ABC.
So, area of the triangle ABC is
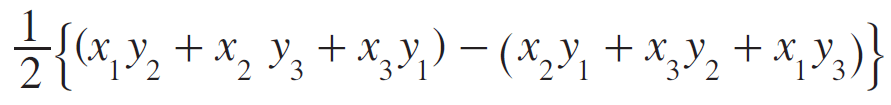
Example 1 :
Find the area of triangle whose vertices are (-3, -9), (-1, 6) and (3, 9).
Solution :
First we have to plot the point in the graph sheet as below.
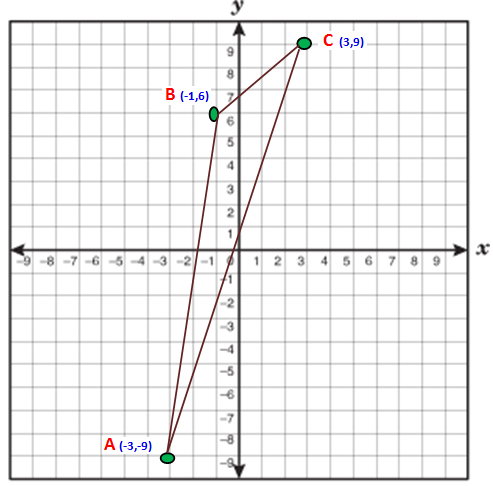
Now we have to take anticlockwise direction. So we have to take the points in the order C (3, 9) B (-1, 6) and A (-3, -9)

Area of the triangle CBA
= (1/2) {(18 + 9 - 18) - (-9 - 18 - 27)}
= (1/2) {9 - ( -54)}
= (1/2) {9 + 54}
= (1/2) (63)
= (63/2)
= 31.5 Square units.
Therefore the area of CBA = 31.5 square units.
Example 2 :
Find the area of triangle whose vertices are (-3, -9) (3, 9) and (5, -8).
Solution :
First we have to plot the point in the graph sheet as below.
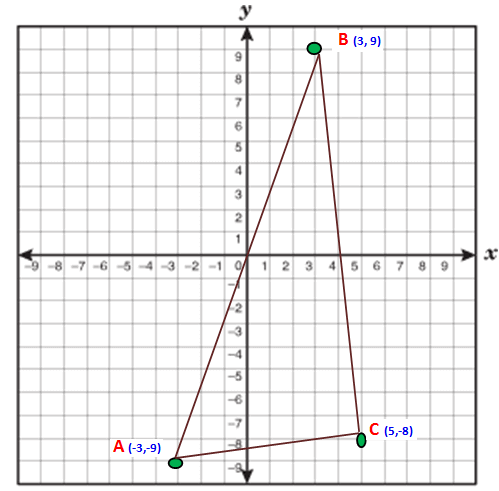
Now we have to take anticlockwise direction. So we have to take the points in the order B (3, 9) A (-3, -9) and C (5, -8)
x1 = 3 x2 = -3 x3 = 5
y1 = 9 y2 = -9 y3 = -8

Area of the triangle BAC
= (1/2) {(-27 - 24 + 45) - (-27 - 45 - 24)}
= (1/2) {(-51 + 45) - (-96)}
= (1/2) {-6 + 96}
= (1/2) (90)
= (90/2)
= 45 Square units.
Therefore the area of BAC = 45 square units.
Example 3 :
Find the area of triangle whose vertices are (4, 5) (4, 2) and (-2, 2).
Solution :
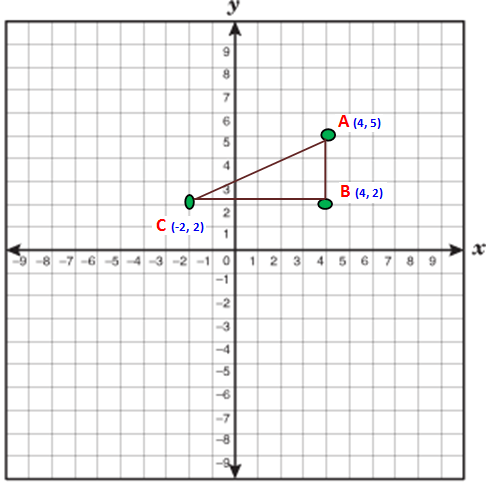
Now we have to take anticlockwise direction. So we have to take the points in the order A (4, 5) C (-2, 2) and B (4, 2)
x1 = 4 x2 = -2 x3 = 4
y1 = 5 y2 = 2 y3 = 2

Area of the triangle ACB
= (1/2) {(8 - 4 + 20) - (-10 + 8 + 8)}
= (1/2) {(28 - 4) - ( -10 + 16)}
= (1/2) (24 - 6)
= (1/2) x 18
= (18/2)
= 9 Square units.
Therefore the area of ACB = 9 square units
Example 4 :
Find the area of triangle whose vertices are (3, 1) (2, 2) and (2, 0).
Solution :
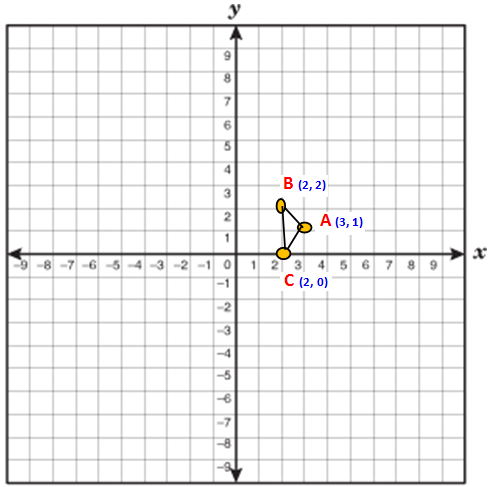
Now we have to take anticlockwise direction. So we have to take the points in the order B (2, 2) C (2, 0) and A (3, 1)
x1 = 2 x2 = 2 x3 = 3
y1 = 2 y2 = 0 y3 = 1

Area of the triangle BCA
= (1/2) {(0 + 2 + 6) - (4 + 0 + 2)}
= (1/2) {8 - 6}
= (1/2) (2)
= (2/2)
= 1 Square units.
Therefore the area of ACB = 1 square units.
Example 5 :
Find the area of triangle whose vertices are (3, 1) (0, 4) and (-3, 1).
Solution :
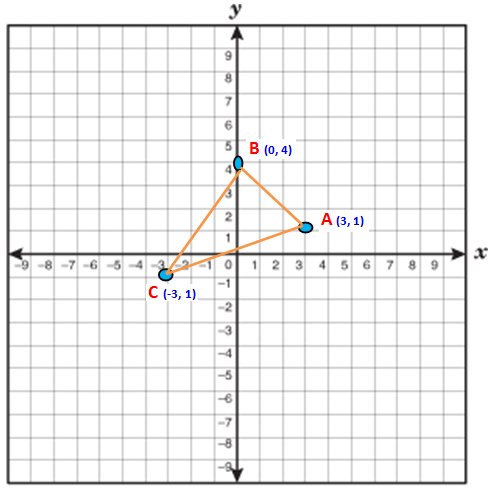
Now we have to take anticlockwise direction. So we have to take the points in the order B (0, 4) C (-3, 1) and A (3, 1).
x1 = 0 x2 = -3 x3 = 3
y1 = 4 y2 = 1 y3 = 1

Area of the triangle BCA
= (1/2) {(0 -3 + 12) - (-12 + 3 + 0)}
= (1/2) {9 - ( -12 + 3)}
= (1/2) {9 - (-9) }
= (1/2) {9 + 9)}
= (1/2) x 18
= 9 Square units.
Therefore the area of BCA = 9 square units.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number

