FIND ORTHOCENTER OF A TRIANGLE WITH GIVEN VERTICES
Here we are going to see how to find orthocenter of a triangle with given vertices.
What is Orthocenter ?
It can be shown that the altitudes of a triangle are concurrent and the point of concurrence is called the orthocentre of the triangle.The orthocentre is denoted by O.
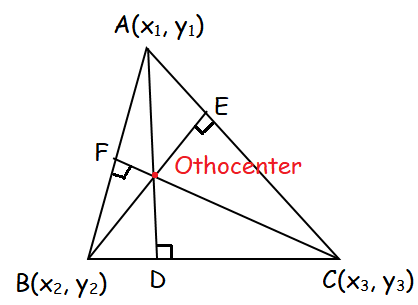
Let ABC be the triangle AD,BE and CF are three altitudes from A, B and C to BC, CA and AB respectively.
Steps Involved in Finding Orthocenter of a Triangle :
- Find the equations of two line segments forming sides of the triangle.
- Find the slopes of the altitudes for those two sides.
- Use the slopes and the opposite vertices to find the equations of the two altitudes.
- Solve the corresponding x and y values, giving you the coordinates of the orthocenter.
Finding Orthocenter of a Triangle - Examples
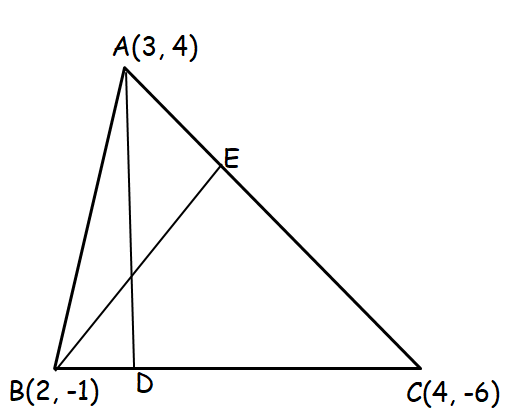
Example 1 :
Find the co ordinates of the orthocentre of a triangle whose vertices are (3, 4) (2, -1) and (4, -6).
Solution :
Let the given points be A (3, 4) B (2, -1) and C (4, -6)
Slope of AC = [(y2 - y1)/(x2 - x1)]
A (3, 4) and C (4, -6)
here x1 = 3, x2 = 4, y1 = 4 and y2 = -6
= [(-6-4)/(4-3)]
= (-10)/1
= -10
Slope of the altitude BE = -1/ slope of AC
= -1/(-10)
= 1/10
Equation of the altitude BE :
(y - y1) = m (x -x1)
Here B (2, -1) and m = 1/10
(y - (-1)) = 1/10 (x - 2)
10 (y + 1) = (x - 2)
10y + 10 = x - 2
x - 10y - 2 - 10 = 0
x - 10y - 12 = 0
x - 10y - 12 = 0
x = 10y + 12 --------(1)
Slope of BC = (y2 - y1)(x2 - x1)]
B (2,-1) and C (4,-6)
here x₁ = 2,x₂ = 4,y₁ = -1 and y₂ = -6
= [(-6 - (-1))/(4 - 2)]
= (-6 + 1)/2
= -5/2
Slope of the altitude AD = -1/ slope of AC
= -1/(-5/2)
= 2/5
Equation of the altitude AD :
(y - y1) = m (x - x1)
Here A(3, 4) m = 2/5
(y - 4) = 2/5 (x - 3)
5(y - 4) = 2(x - 3)
5y - 20 = 2x - 6
2x - 5y - 6 + 20 = 0
2x - 5y + 14 = 0 --------(2)
Substituting (1) into (2), we get
2(10y + 12) - 5y + 14 = 0
20y + 24 - 5y + 14 = 0
15y + 38 = 0
15y = -38
y = -38/15
By applying y = -38/15 in (1), we get
x = 10(-38/15) + 12
x = -76/3 + 12
x = -40/3
Therefore the orthocenter is (-40/3, -38/15).

After having gone through the stuff given above, we hope that the students would have understood how to find the orthocenter of a triangle with given vertices.
If you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number

