CIRCUMCENTER OF A TRIANGLE WORKSHEET
Problem 1 :
Find the co ordinates of the circumcenter of a triangle whose vertices are (2, -3), (8, -2) and (8, 6).
Problem 2 :
Find the co ordinates of the circumcenter of a triangle whose vertices are (0, 4), (3, 6) and (-8, -2).

Detailed Answer Key
Problem 1 :
Find the co ordinates of the circumcenter of a triangle whose vertices are (2, -3), (8, -2) and (8, 6).
Solution :
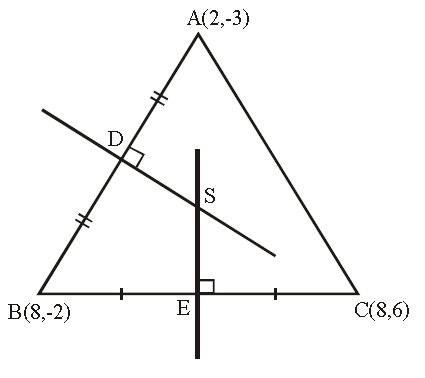
Let A(2, -3), B(8, -2) and C(8, 6) be the vertices of the triangle.
D is the midpoint of AB and E is the midpoint of BC.
Midpoint of AB is
= [(x1 + x2)/2, (y1 + y2)/2]
Substitute (x1, y1) = (2, -3) and (x2, y2) = (8, -2).
= [(2 + 8)/2, (-3 - 2)/2]
= [10/2, -5/2]
= (5, -5/2)
So, the point D is (5, -5/2).
Slope of AB is
= [(y2 - y1)/(x2 - x1)]
Substitute (x1, y1) = (2, -3) and (x2, y2) = (8, -2).
= [(-2 - (-3)] / (8 - 2)
= (-2 + 3) / 6
= 1/6
Slope of the perpendicular line to AB is
= -1 / slope of AB
= -1 / (1/6)
= -1 ⋅ (6/1)
= -6
Equation of the perpendicular bisector to the side AB :
y = mx + b
Substitute m = -6.
y = -6x + b -----(1)
Substitute the point D(5, -5/2) for (x, y) into the above equation.
-5/2 = -6(5) + b
-2.5 = -30 + b
Add 30 to each side.
27.5 = b
Substitute b = 27.5 in (1).
(1)-----> y = -6x + 27.5
Equation of the perpendicular line through D is
y = -6x + 27.5 -----(2)
Midpoint of BC is
= [(x1 + x2)/2, (y1 + y2)/2]
Substitute (x1, y1) = (8, -2) and (x2, y2) = (8, 6).
= [(8 + 8)/2, (-2 + 6)/2]
= [16/2, 4/2]
= (8, 2)
So, the point E is (8, 2).
Slope of BC is
= [(y2 - y1)/(x2 - x1)]
Substitute (x1, y1) = (8, -2) and (x2, y2) = (8, 6).
= [6 - (-2)] / (8 - 8)
= (6 + 2) / 0
= 8/0
Slope of the perpendicular line to BC is
= -1 / slope of BC
= -1 / (8/0)
= -1 ⋅ (0/8)
= -1 ⋅ 0
= 0
Equation of the perpendicular bisector to the side BC :
y = mx + b
Substitute m = 0.
y = b -----(3)
Substitute the point E(8, 2) for (x, y) into the above equation.
2 = b
Substitute b = 2 in (1).
(1)-----> y = 2
Equation of the perpendicular line through D is
y = 2 -----(4)
Solving (2) and (4), we get
x = 4.25 and y = 2
Therefore, the circumcenter of the triangle ABC is
(4.25, 2)
Problem 2 :
Find the co ordinates of the circumcenter of a triangle whose vertices are (0, 4), (3, 6) and (-8, -2).
Solution :
We can follow the steps done in the above problem and get the circumcenter of the triangle.
So, the circumcenter of the triangle with vertices (0, 4), (3, 6) and (-8, -2) is
(69.5, -97)

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Printable Math Worksheets
Apr 20, 24 12:02 AM
Printable Math Worksheets - Worksheets in Pdf formats from grade 1 to 10 -
Printable Math Worksheets for Grade 2
Apr 19, 24 11:58 PM
Printable Math Worksheets for Grade 2 -
Sequences and Series
Apr 19, 24 11:45 PM
Sequences and Series - Concept - Examples