FACTORING HIGHER DEGREE POLYNOMIALS WITH SYNTHETIC DIVISION
Factoring Higher Degree Polynomials with Synthetic Division :
To solve a polynomial of degree 5, we have to factor the given polynomial as much as possible. After factoring the polynomial of degree 5, we find 5 factors and equating each factor to zero, we can find the all the values of x.
Example 1 :
Solve
x5 - 5x4 + 9x3 - 9x2 + 5x - 1
Solution :
Since the degree of the polynomial is 5, we have 5 zeroes. To find the zeroes, we use synthetic division.

The other roots are given by
x4 - 4 x3 + 5 x2 - 4x + 1 = 0
Dividing the entire equation by x²
x⁴/x² - 4 x³/x² + 5 x²/x² - 4 x/x² + 1/x² = 0
1 x² - 4 x - 5 - 4 (1/x) + (1/x²) = 0
1 (x² + 1/x²) - 4 (x + 1/x) + 5 = 0 ------ (1)
Let x + 1/x = y
To find the value of x² + 1/x² from this we have to take squares on both sides
(x + 1/x)² = y²
x² + 1/x² + 2 x (1/x) = y²
x² + 1/x² + 2 = y²
x² + 1/x² = y² - 2
So we have to plug y² - 2 instead of x² + 1/x²
Let us plug this value in the first equation
1(y² - 2) - 4y + 5 = 0
y² - 2 - 4y + 5 = 0
1y² - 4y - 2 + 5 = 0
1y² - 4y + 3 = 0
(y - 1) (y - 3) = 0
Solving for y, we get
y - 1 = 0 and y - 3 = 0
y = 1 and y = 3
When y = 1
x + 1/x = y
(x² + 1)/x = 1
(x² + 1) = 1 x
x² - 1x + 1 = 0
Solving the quadratic equation using the formula
x = (-b ± √b2 - 4ac)/2a
By comparing the quadratic equation with the general form of a quadratic equation ax2 + bx + c = 0, we get
a = 1, b = -1 and c = 1
b2 - 4ac = (-1)2 - 4(1)(1)
= -3
So,
x = (1 ± √-3)/2
x = (1 ± √3i)/2
When y = 3
x + 1/x = y
(x² + 1)/x = 3
(x² + 1) = 3x
x² - 3x + 1 = 0
Solving the quadratic equation using the formula
x = (-b ± √b2 - 4ac)/2a
By comparing the quadratic equation with the general form of a quadratic equation ax2 + bx + c = 0, we get
a = 1, b = -3 and c = 1
b2 - 4ac = (-3)2 - 4(1)(1)
= 5
So,
x = (1 ± √5)/2
Hence the values of x are (1 ± √-3)/2, (1 ± √5)/2 and 1.
Example 2 :
Solve
x5 - 5x3 + 5x2 - 1
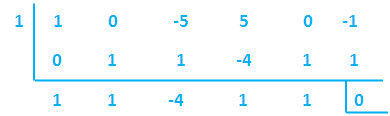
Dividing the entire equation by x²
x⁴/x² + x³/x² - 4 x²/x² + x/x² + 1/x² = 0
x² + x - 4 + 1/x + 1/x² = 0
(x² + 1/x²) - 4 + (1/x) + x = 0
(x² + 1/x²) + (x + 1/x) - 4 = 0 ------ (1)
Let x + 1/x = y
To find the value of x² + 1/x² from this we have to take squares on both sides
(x + 1/x)² = y²
x² + 1/x² + 2 x (1/x) = y²
x² + 1/x² + 2 = y²
x² + 1/x² = y² - 2
So we have to plug y² - 2 instead of x² + 1/x²
Let us plug this value in the first equation
(y² - 2) + y - 4 = 0
y² - 2 + y - 4 = 0
y² + y - 6 = 0
(y + 3) (y - 2) = 0
Solving for y, we get
y + 3 = 0 and y - 2 = 0
y = -3 and y = 2
When y = -3
x + 1/x = y
(x² + 1)/x = -3
(x² + 1) = -3 x
x² + 1 + 3x = 0
x² + 3x + 1 = 0
Solving the quadratic equation using the formula
x = (-b ± √b2 - 4ac)/2a
By comparing the quadratic equation with the general form of a quadratic equation ax2 + bx + c = 0, we get
a = 1, b = 3 and c = 1
b2 - 4ac = 32 - 4(1)(1)
= 5
x = (-1 ± √5)/2
When y = 2
x + 1/x = y
(x² + 1)/x = 2
(x² + 1) = 2x
x² - 2x + 1 = 0
(x - 1) (x - 1) = 0
Solving for x, we get
x = 1
Therefore the 5 roots are x = 1, 1, 1, (-3 ± √5)/2.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
