WORD PROBLEMS INVOLVING ANGLE OF ELEVATION IN TRIGONOMETRY
Problem 1 :
A lamp-post stands at the centre of a circular park. Let P and Q be two points on the boundary such that PQ subtends an angle 90° at the foot of the lamp-post and the angle of elevation of the top of the lamp post from P is 30° . If PQ = 30 m, then find the height of the lamp post.
Solution :
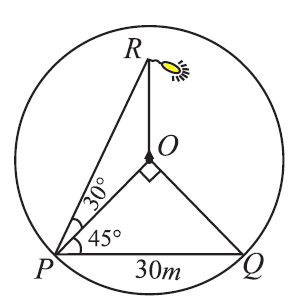
Let O be the centre of the park and OR be the lamp post. P and Q are two points on the boundary of the circular park. Given that PQ = 30m,
∠POQ = 90°
In a right triangle OPQ, ∠POQ = 90°
OP = OQ = radius. So ∠OPQ = ∠OPQ = 45°
OP = PQ x cos 45°
OP = 30/√2 ==> (30/√2) x (√2/√2) ==> 15 √2
In a triangle RPO
tan 30° = OR/OP
1/√3 = OR/15√2
OR = (15√2/√3) ==> (15√2/√3) x (√3/√3)
= 15√6/3 ==> 5√6
So, the height of the lamp post is 5√6 m.
Problem 2 :
A person in an helicopter flying at a height of 700 m, observes two objects lying opposite to each other on either bank of a river. The angles of depression of the objects are 30° and 45°. Find the width of the river. (√3 = 1.732 )
Solution :
From the given information, we can draw a rough diagram
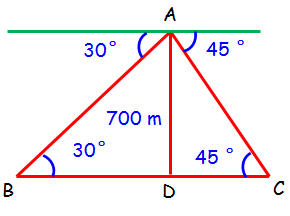
AD = 700 m
In triangle ACD, we need to find the length of DC.
∠ACD = 45°
tan θ = opposite side/Adjacent side
tan 45° = AD/DC
1 = 700/DC ==> DC = 700 --(1)
In triangle ABD, we need to find the length of BD.
∠ABD = 30°
tan θ = opposite side/Adjacent side
tan 30° = AD/BD
1/√3 = 700/BD ==> BD = 700√3 --(2)
(1) + (2)
Width of the river = BD + DC ==> 700 + 700√3
= 700(1 + √3) ==> 700 (1 + 1.732) = 700 (2.732)
= 1912.4 m
Width of the river is 1912.4 m.
Problem 3 :
A person X standing on a horizontal plane, observes a bird flying at a distance of 100 m from him at an angle of elevation of 30°. Another person Y standing on the roof of a 20 m high building, observes the bird at the same time at an angle of elevation of 45°. If X and Y are on the opposite sides of the bird, then find the distance of the bird from Y.
Solution :
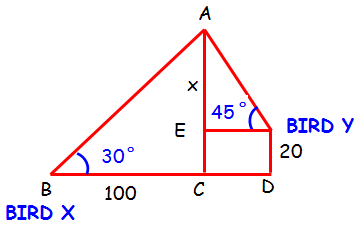
In triangle ABC
∠ABC = 30°
sin θ = opposite side/Hypotenuse side
sin 30° = (AE + EC)/BC
1/2 = (x + 20)/100
100 = 2 (x + 20)
100 = 2x + 40
100 - 40 = 2x ==> 2x = 60 ==> x = 30
In triangle AYE
∠AYE = 45°
sin 45° = AE /EY
1/√2 = x / EY
1/√2 = 30 / EY
EY = 30√2
So, the required distance of the bird from Y is 30√2 m.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
