EQUATION OF THE LINE PASSING THROUGH A POINT AND INTERCEPTS

Example 1 :

Find the equation of the straight line passing through the point (5, -3) and whose intercepts on the axes are equal in magnitude but opposite in sign.

Solution :

Intercepts on the axes are equal in magnitude but opposite in sign.

x-intercept(a) = k and y-intercept(b) = -k

(x/a) + (y/b)  =  1

(x/k) + (y/(-k))  =  1

The straight line is passing through the point (5, -3)

(5/k) + (-3)/(-k) = 1

(5/k) + (3/k) = 1

(5 + 3)/k = 1 ==>  8/k = 1 ==> k = 8

a = 8 , b = -8

Equation of the line :

(x/a) + (y/b) = 1

(x/8) + (y/(-8)) = 1

(x - y)/8 = 1

x - y = 8

x - y - 8 = 0

Example 2 :

Find the equation of the line passing through the point (9, -1) and having its x-intercept thrice as its y-intercept.

Solution :

x - intercept (a) = 3b 

(x/a) + (y/b)  =  1

(x/3b) + (y/b)  =  1

The straight line is passing through the point (9, -1)

(9/3b) + (-1/b)  =  1

(3/b) + (-1/b) = 1

(3 - 1)/b = 1

2/b = 1

b = 2 

So a = 3(2) = 6

Equation of the line :

(x/a) + (y/b) = 1

(x/6) + (y/2) = 1

(x + 3y)/6 = 1

 x + 3y = 6

x + 3y - 6 = 0

Example 3 :

A straight line cuts the coordinate axes at A and B. If the midpoint of AB is (3, 2), then find the equation of AB.

Solution :

Let us a draw rough diagram for the given information.

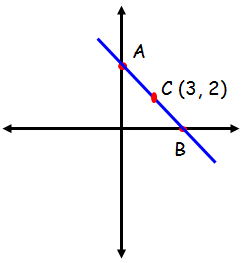
Let "C" be the midpoint of the line joining the points A and B.

The required line intersects the x-axis at the point B and y-axis at A. So let us consider the point B as (a, 0) and A as (0, b)

Midpoint of AB = (x₁ + x₂)/2, (y₁ + y₂)/2

 (a + 0)/2, (0 + b)/2  =  (3, 2)

 a/2, b/2  =  (3, 2)

equating the x and y co-ordinates 

a/2 = 3   b/2 = 2

a = 6 and b = 4

A (0,4) and B (6, 0)

Equation of the line AB :

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

(y-4)/(0-4)  =  (x-0)/(6-0)

(y-4)/(-4)  =  x/6

6(y - 4) = -4x

 6y - 24 = -4x

4x + 6y - 24 = 0

Divide the whole equation by 2, we get

2x + 3y - 12 = 0 

Hence the required equation is 2x + 3y - 12 = 0 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.