SIMILAR TRIANGLES PROBLEMS WITH ANSWERS
Problem 1 :
P and Q are points on sides AB and AC respectively, of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.
Solution :
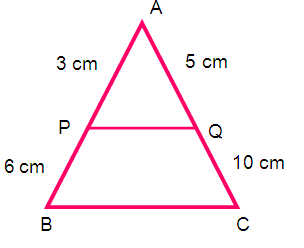
AP/PB = AQ/AC
3/9 = 5/15
1/3 = 1/3
In triangles APQ, and ABC we get
(AP/AB) = (AQ/AC)
∠ A = ∠A
By using SAS criterion ∆ APQ ~ ∆ ABC
(AP/AB) = (Q/AC) = (PQ/BC)
(AP/PB) = (PQ/BC)
PQ/BC = 3/9
PQ/BC = 1/3
3 PQ = BC
BC = 3 PQ
Problem 2 :
In triangle ABC, AB = AC and BC = 6 cm. D is a point on the side AC such that AD = 5 cm and CD = 4 cm. Show that triangle BCD and triangle ACB are congruent and hence find BD.
Solution :
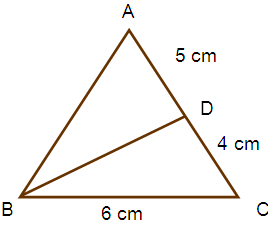
In triangle ABC, AB = AC
(BC/AC) = (CD/CB)
(6/9) = (4/6)
From the triangles ∆ BCD, ∆ ACB we get
(BC/AC) = (CD/CB)
∠ C = ∠ C (Common angle)
By using SAS criterion, we get
∆ BCD ~ ∆ ACB
(BD/AB) = (BC/AC)
Here, AB = AC
BD/AC = 6/9
BD/9 = 6/9
BD = 6 cm
Problem 3 :
The points D and E are on the sides AB and AC of triangle ABC respectively, such that DE and BC are parallel. If AB = 3 AD and the area triangle ABC is 72 cm², then find the area of the quadrilateral DBCE.
Solution :
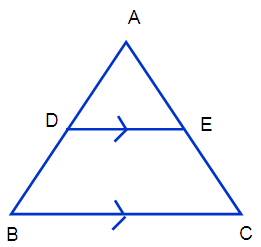
From the diagram,
the sides DE and BC are parallel and AB = 3 AD
(AD/AB) = 1/3
By taking the two triangles, ∆ ADE and ∆ ABC
∠ ADE = ∠ ABC
∠A = ∠A (Common angle)
By using AA similarity criterion ∆ADE ~ ∆ABC
Area of ∆ ADE/Area of ∆ ABC = AD²/AB²
Area of ∆ ADE/72 = 1/9
Area of ∆ ADE = (1/9) ⋅ 72 = 8 cm
Area of quadrilateral = area of ∆ ABC – Area of ∆ DE
= 72 – 8
= 64 cm2
Therefore the required area of quadrilateral is 64 cm2.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
