SOLVING WORD PROBLEMS WITH SIMILAR TRIANGLES

Problem 1 :

A girl is in the beach with her father. She spots a swimmer drowning. She shouts to her father who is 50 m due west of her. Her father is 10 m nearer to a boat than the girl. If her father uses the boat to reach the swimmer, he has to travel a distance 126 m from the boat. At the same time, the girl spots a man riding a water craft who is 98 m away from the boat. The man n the water craft is due east of the swimmer. How far must the man travel to rescue the swimmer?

Solution :

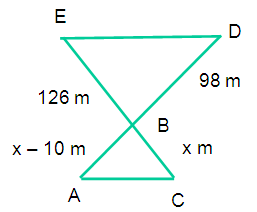
Let “A” be the place where her father is standing 

Let “C” be the place where a girl is standing

Let “B” be the place where the boat is

Let D” be the place where water craft is

Let “E” be the place where the swimmer is

BC  =  x m

AB  =  (x - 10) m

By considering he triangles ∆ ABC, ∆ DBE

∠ABC  =  ∠DBE (vertically opposite angles)

∠BAC  =  ∠BDE (alternate angles)

By using AA similarity criterion ∆ ABC ~ ∆ DBE

(AB/DB)  =  (BC/BE)  =  (AC/DE)

(AB/DB)  =  (BC/BE)

(x – 10)/98  =  x/126

126 (x – 10)  =  98 x

126 x – 1260  =  98 x

126 x – 98 x  =  1260

28 x  =  1260

   x  =  1260/28

   x  =  45

   BC  =  45 m

Also, (BC/BE)  =  (AC/DE)

DE  =  (AC x BE)/BC

  =  (50 x 126)/45

  =  6300/45

  =  140 m

The man has to travel 140 m to rescue the swimmer.

Problem 2 :

P and Q are points on sides AB and AC respectively, of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ.

Solution :

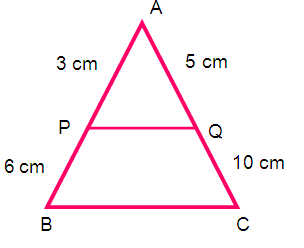
AP/PB  =  AQ/AC

3/9  =  5/15

1/3  =  1/3

In triangles APQ, and ABC we get

(AP/AB)  =  (AQ/AC)

∠A  =  ∠A

By using SAS criterion ∆ APQ ~ ∆ ABC

(AP/AB)  =  (Q/AC)  =  (PQ/BC)

(AP/PB)  =  (PQ/BC)

PQ/BC  =  3/9

PQ/BC  =  1/3

3PQ  =  BC

BC  =  3PQ  

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.