EXAMPLES OF BASIC PROPORTIONALITY THEOREM
Basic Proportionality Theorem :
If a straight line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
Converse of Basic Proportionality Theorem Examples :
If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Given :
In triangle ABC and a line intersecting AB in D and AC in E, such that AD/DB = AE/EC.
Example 1 :
In the figure AP = 3 cm, AR = 4.5 cm, AQ = 6 cm, AB = 5 cm and AC = 10 cm. Find the length of AD.
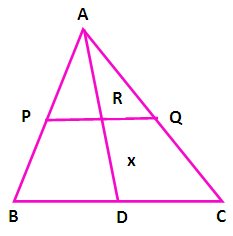
Solution :
From the given information we get, AB/AP = AC/AQ.
In triangle ABC,
AB/AP = AC/AQ
By using converse of “Thales theorem” PQ is parallel to BC.
RD = x
In triangle ABD, PR is parallel to BD
AD = AR + RD
AD = 4.5 + x
AB/AP = AD/AR
5/3 = (4.5 + x)/4.5
(5 ⋅ 4.5)/3 = 4.5 + x
7.5 = 4.5 + x
x = 7.5 – 4.5
x = 3
Here we need to find the length of AD = 4.5 + x
= 4.5 + 3
= 7.5 cm
Example 2 :
E and F are points on the sides PQ and PR respectively, of a triangle PQR. For each of the following cases. Verify EF is parallel to QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Solution :
First let us draw the picture for the above details
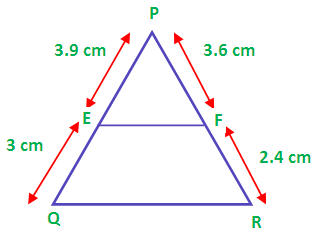
To verify whether EF is parallel to QR we have to check the condition
PE/EQ = PF/FR
3.9/3 = 3.6/2.4
1.3 ≠ 1.5
So the sides EF and QR are not parallel.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Solution :
First let us draw the picture for the above details
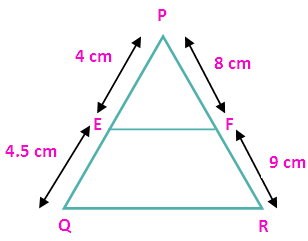
To verify whether EF is parallel to QR we have to check the condition
PE/EQ = PF/FR
4/4.5 = 8/9
0.88 = 0.88
So the sides EF and QR are parallel.
Example 3 :
In the figure, AC is parallel to BD and CF is parallel to DF, if OA = 12 cm, AB = 9 cm, OC = 8 cm and EF= 4.5 cm, then find FQ.
Solution :
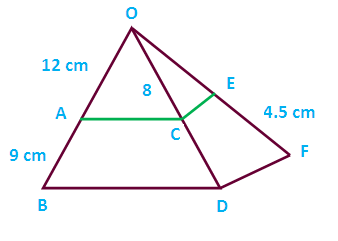
In triangle OBD, AC is parallel to BD. By using “Thales theorem” we get,
OA/AB = OC/CD
12/9 = 8/CD
CD = (8 x 9)/12
= 72/12
= 6 cm
In triangle ODF, the sides CE and DF are parallel, by using “Thales theorem” we get,
OC/CD = OE/EF
8/6 = OE/4.5
OE = (8 ⋅ 4.5)/6
= 36/6
= 6 cm
So, OF = OE + EF
= 6 + 4.5
= 10.5 cm
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
