FINDING DISTANCE BETWEEN TWO POINTS EXAMPLES
Let (x1, y1) and (x2, y2) be the two points as shown below.

Then, the formula for the distance between the two points is
√[(x2 - x1)2 + (y2 - y1)2]
Examples
Example 1 :
Check whether (5,-2) (6,4) and (7,-2) are the vertices of an isosceles triangle.
Solution :
Let the given points as A(5,-2) B(6,4) and C(7,-2)
Distance between two points = √(x2 - x1)2 + (y2 - y1)2
Length of the side AB :
Here, x1 = 5, y1 = -2, x2 = 6 and y₂ = 4
= √(6 - 5)2 + (4 - (-2))2
= √12 + (4+2)2
= √1 + 36
= √37
Length of the side BC :
Here, x1 = 6, y1 = 4, x2 = 7 and y₂ = -2
= √(7 - 6)2 + (-2 - 4)2
= √12 + (-6)2
= √1 + 36
= √37
Length of the side CA :
Here, x1 = 7, y1 = -2, x2 = 5 and y₂ = -2
= √(-5 - 7)2 + (-2 - (-2))2
= √(-12)2 + (-2 + 2)2
= √144 + 0
= √144
= 12
AB = BC
Since length of two sides are equal, the given points are the vertices of a triangle.
Example 2 :
In a classroom 4 friends are seated at the points A,B,C and D as shown in figure given below. Champa and Chameli walk into the class and after observing for a few minutes champa asks Chameli,"Don't you think ABCD is a square?" Chameli disagrees. Using distance formula, find which of them is correct.
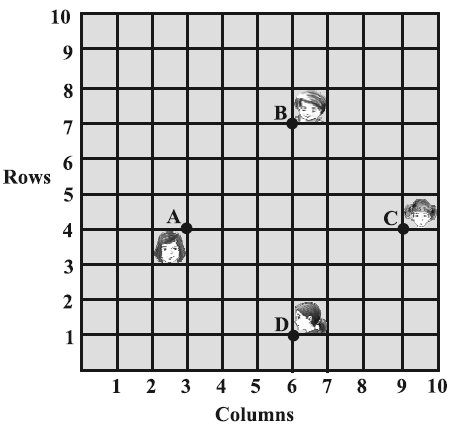
Solution :
It can be observed that A (3, 4) , B (6, 7), C(9, 4) and D(6, 1) are the position of these 4 friends.
Length of AB :
Here, x1 = 3, y1 = 4, x2 = 6 and y2 = 7
= √(6 - 3)2 + (7 - 4)2
= √(3)2 + (3)2
= √9 + 9
= √18
= 3√2
Length of BC :
Here, x1 = 6, y1 = 7, x2 = 9 and y2 = 4
= √(9 - 6)2 + (4 - 7)2
= √(3)² + (-3)²
= √(9 + 9)
= √18
= 3√2
Length of CD :
Here, x1 = 9, y1 = 4, x2 = 6 and y2 = 1
= √(6 - 9)² + (1 - 4)²
= √(-3)² + (-3)²
= √9 + 9
= √18
= 3√2
Length of DA :
Here, x1 = 6, y1 = 1, x2 = 3 and y2 = 4
= √(3 - 6)² + (4 - 1)²
= √(-3)² + (3)²
= √9 + 9
= √18
= 3√2
Length of diagonal AC :
Here, x1 = 3, y1 = 4, x2 = 9 and y2 = 4
= √(9 - 3)2 + (4 - 4)2
= √62 + 02
= √36
= 6
Length of diagonal BD :
Here, x1 = 6, y1 = 7, x2 = 6 and y2 = 1
= √(6 - 6)2 + (1 - 7)2
= √02 + (-6)2
= √36
= 6
It can be observed that all the sides of this quadrilateral ABCD are the same length and also the diagonals are of the same length.
Therefore, ABCD is a square. Hence, Champa was correct.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
