WORD PROBLEMS ON SETS AND VENN DIAGRAMS

Basic Stuff

To understand, how to solve Venn diagram word problems with 3 circles, we have to know the following basic stuff.  

u ----> union (or)

n ----> intersection (and)

Addition Theorem on Sets

Theorem 1 :

n(AuB) = n(A) + n(B) - n(AnB)

Theorem 2 :

n(AuBuC) :

=n(A) + n(B) + n(C) - n(AnB) - n(BnC) - n(AnC) + n(AnBnC)

Explanation :

Let us come to know about the following terms in details.

n(AuB) = Total number of elements related to any of the two events A & B.

n(AuBuC) = Total number of elements related to any of the three events A, B & C.

n(A) = Total number of elements related to A

n(B) = Total number of elements related to B

n(C) = Total number of elements related to C

For  three events A, B & C, we have

n(A) - [n(AnB) + n(AnC) - n(AnBnC)] :

Total number of elements related to A only

n(B) - [n(AnB) + n(BnC) - n(AnBnC)] :

Total number of elements related to B only

n(C) - [n(BnC) + n(AnC) + n(AnBnC)] :

Total number of elements related to C only

n(AnB) :

Total number of elements related to both A & B

n(AnB) - n(AnBnC) :

Total number of elements related to both (A & B) only

n(BnC) :

Total number of elements related to both B & C

n(BnC) - n(AnBnC) :

Total number of elements related to both (B & C) only

n(AnC) :

Total number of elements related to both A & C

n(AnC) - n(AnBnC) :

Total number of elements related to both (A & C) only

For  two events A & B, we have

n(A) - n(AnB) :

Total number of elements related to A only

n(B) - n(AnB) :

Total number of elements related to B only

Practice Problems

Problem 1 :

In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Find how many had taken one course only.

Solution :

Step 1 :

Let M, C, P represent sets of students who had taken mathematics, chemistry and physics respectively.

Step 2 :

From the given information, we have

n(M) = 64, n(C) = 94, n(P) = 58,

n(MnP) = 28, n(MnC) = 26, n(CnP) = 22

n(MnCnP) = 14

Step 3 :

From the basic stuff, we have

Number of students who had taken only Math

= n(M) - [n(MnP) + n(MnC) - n(MnCnP)]

= 64 - [28 + 26 - 14]

= 64 - 40

= 24

Step 4 :

Number of students who had taken only Chemistry :

= n(C) - [n(MnC) + n(CnP) - n(MnCnP)]

= 94 - [26+22-14]

= 94 - 34

= 60

Step 5 :

Number of students who had taken only Physics :

= n(P) - [n(MnP) + n(CnP) - n(MnCnP)]

= 58 - [28 + 22 - 14]

= 58 - 36

= 22

Step 6 :

Total number of students who had taken only one course :

= 24 + 60 + 22

= 106

Hence, the total number of students who had taken only one course is 106.

Alternative Method (Using venn diagram) :

Step 1 :

Venn diagram related to the information given in the question:

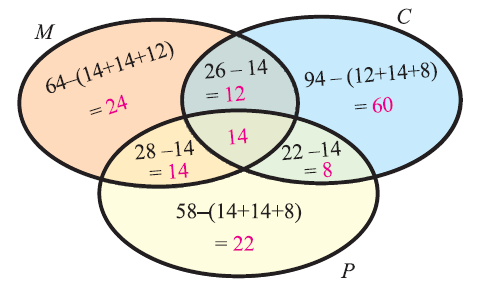
Step 2 :

From the venn diagram above, we have

Number of students who had taken only math = 24

Number of students who had taken only chemistry = 60

Number of students who had taken only physics = 22

Step 3 :

Total Number of students who had taken only one course :

= 24 + 60 + 22

= 106

Hence, the total number of students who had taken only one course is 106.

Problem 2 :

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).

Solution :

Step 1 :

Let F, H and C represent the set of students who play foot ball, hockey and cricket respectively.

Step 2 :

From the given information, we have

n(F) = 65, n(H) = 45, n(C) = 42,

n(FnH) = 20, n(FnC) = 25, n(HnC) = 15

n(FnHnC) = 8

Step 3 :

From the basic stuff, we have

Total number of students in the group is n(FuHuC).

n(FuHuC) is equal to

= n(F) + n(H) + n(C) - n(FnH) - n(FnC) - n(HnC) + n(FnHnC)

n(FuHuC) = 65 + 45 + 42 -20 - 25 - 15 + 8

n(FuHuC) = 100

Hence, the total number of students in the group is 100.

Alternative Method (Using Venn diagram) :

Step 1 :

Venn diagram related to the information given in the question :

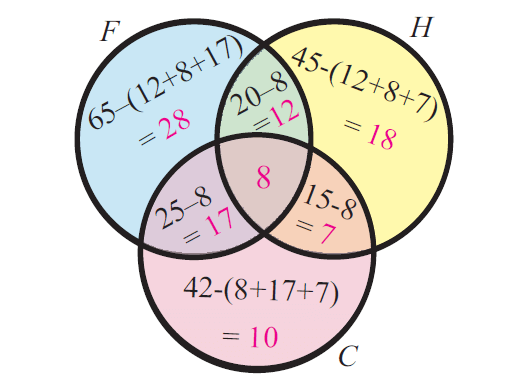
Step 2 :

Total number of students in the group :

= 28 + 12 + 18 + 7 + 10 + 17 + 8

= 100

So, the total number of students in the group is 100.

Problem 3 :

In a college, 60 students enrolled in chemistry,40 in physics, 30 in biology, 15 in chemistry and physics,10 in physics and biology, 5 in biology and chemistry. No one enrolled in all the three. Find how many are enrolled in at least one of the subjects.

Solution :

Let C, P and B represents the subjects Chemistry, Physics  and Biology respectively.

Number of students enrolled in Chemistry :

n(C) = 60

Number of students enrolled in Physics :

n(P) = 40

Number of students enrolled in Biology :

n(B) = 30

Number of students enrolled in Chemistry and Physics :

n(CnP) = 15

Number of students enrolled in Physics and Biology :

n(PnB) = 10

Number of students enrolled in Biology and Chemistry :

n(BnC) = 5

No one enrolled in all the three. So, we have

n(CnPnB) = 0

The above information can be put in a Venn diagram as shown below.

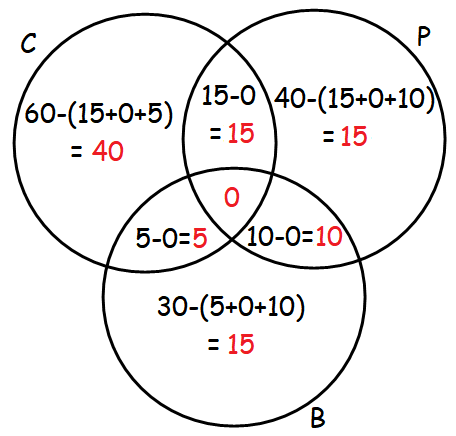
From, the above Venn diagram, number of students enrolled in at least one of the subjects :

= 40 + 15 + 15 + 15 + 5 + 10 + 0

= 100

So, the number of students enrolled in at least one of the subjects is 100.

Problem 4 :

In a town 85% of the people speak Tamil, 40% speak English and 20% speak Hindi. Also 32% speak Tamil and English, 13% speak Tamil and Hindi and 10% speak English and Hindi, find the percentage of people who can speak all the three languages.

Solution :

Let T, E and H represent the people who speak Tamil, English and Hindi respectively.

Percentage of people who speak Tamil :

n(T) = 85

Percentage of people who speak English :

n(E) = 40

Percentage of people who speak Hindi :

n(H)  =  20

Percentage of people who speak English and Tamil :

n(TnE) = 32

Percentage of people who speak Tamil and Hindi :

n(TnH) = 13

Percentage of people who speak English and Hindi :

n(EnH) = 10

Let x be the percentage of people who speak all the three language.

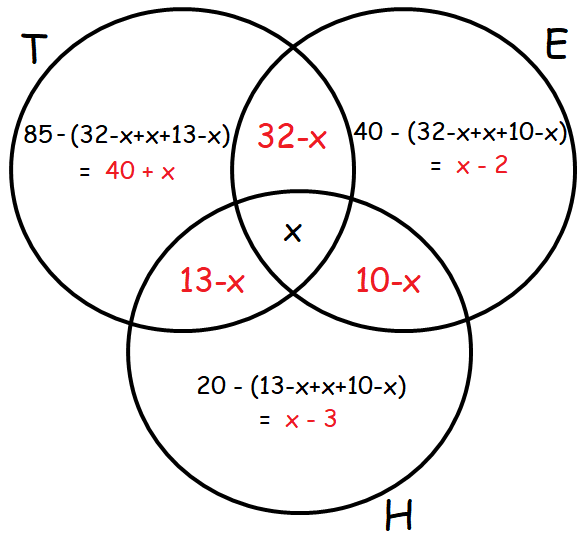
From the above Venn diagram, we can have 

100 = 40 + x + 32 – x + x + 13 – x + 10 – x – 2 + x – 3 + x

100 = 40 + 32 + 13 + 10 – 2 – 3 + x 

100 = 95 – 5 + x

100 = 90 + x

x = 100 - 90

x = 10% 

So, the percentage of people who speak all the three languages is 10%.

Problem 5 :

An advertising agency finds that, of its 170 clients, 115 use Television, 110 use Radio and 130 use Magazines. Also 85 use Television and Magazines, 75 use Television and Radio, 95 use Radio and Magazines, 70 use all the three. Draw Venn diagram to represent these data. Find 

(i) how many use only Radio?

(ii) how many use only Television?

(iii) how many use Television and Magazine but not radio?

Solution :

Let T, R and M represent the people who use Television, Radio and Magazines respectively.

Number of people who use Television :

n(T) = 115

Number of people who use Radio :

n(R) = 110

Number of people who use Magazine :

n(M) = 130

Number of people who use Television and Magazines

n (TnM) = 85

Number of people who use Television and Radio :

n(TnR) = 75

Number of people who use Radio and Magazine :

n(RnM) = 95

Number of people who use all the three :

n(TnRnM) = 70

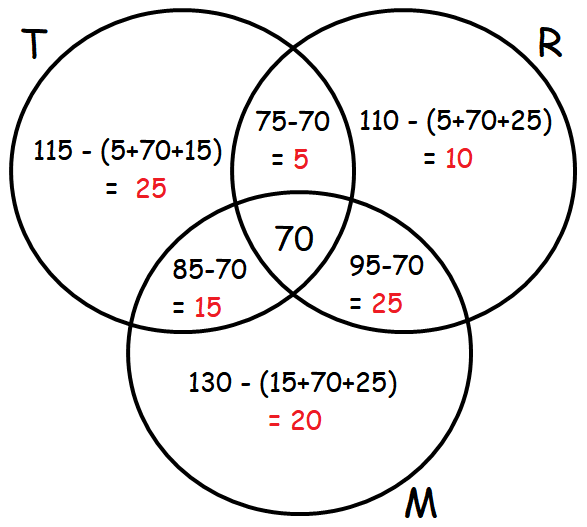
From the above Venn diagram, we have

(i) Number of people who use only Radio is 10.

(ii) Number of people who use only Television is 25.

(iii) Number of people who use Television and Magazine but not radio is 15.

Problem 6 :

In a class of 60 students, 40 students like math, 36 like science, 24 like both the subjects. Find the number of students who like

(i) Math only, (ii) Science only  (iii) Either Math or Science (iv) Neither Math nor science.

Solution :

Step 1 :

Let M and S represent the set of students who like math and science respectively.

Step 2 :

From the information given in the question, we have

n(M) = 40, n(S) = 36, n(MnS) = 24

Step 3 :

Answer (i) :

Number of students who like math only :

= n(M) - n(MnS)

= 40 - 24

= 16

Step 4 :

Answer (ii) :

Number of students who like science only :

= n(S) - n(MnS)

= 36 - 24

=  12

Step 5 :

Answer (iii) :

Number of students who like either math or science :

= n(M or S) 

= n(MuS) 

= n(M) + n(S) - n(MnS)

= 40 + 36 - 24

= 52

Step 6 :

Answer (iv) :

Total number students who like Math or Science subjects :

n(MuS) = 52

Number of students who like neither math nor science

= 60 - 52

= 8

Problem 7 :

At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. Find the number of women doctors attending the conference.

Solution :

Step 1 :

Let M and D represent the set of Indian men and Doctors respectively.

Step 2 :

From the information given in the question, we have

n(M) = 23, n(D) = 4, n(MuD) = 24

Step 3 :

From the basic stuff, we have

n(MuD) = n(M) + n(D) - n(MnD)

24 = 23 + 4 - n(MnD)

n(MnD) = 3 

n(Indian Men and Doctors) = 3

Step 4 :

So, out of the 4 Indian doctors,  there are 3 men.

And the remaining 1 is Indian women doctor.

So, the number women doctors attending the conference is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.