WORD PROBLEMS ON PROFIT AND LOSS
Problem 1 :
Cindy bought 50 pens for $100. She then sold each pen for $2.50. Find the profit or loss percentage.
Solution :
Cost price of 50 pens = $100
Cost price of 1 pen = 100/50 = $2
Selling price of 1 pen = $2.50
Because the selling price of 1 pen is more than cost price of 1 pen, there is profit.
Finding Profit :
Profit = Selling price - Cost price
Profit = 2.50 - 2
Profit = 0.50
Finding Profit Percentage :
Profit % = (Profit/Cost price) ⋅ 100 %
Profit % = (0.50/2) ⋅ 100 %
Profit % = 25 %
Problem 2 :
Jacob purchased a house for $49,000. He spent $6000 for repair and $5,000 for air-conditioning. If he had sold the house $58,000, find the gain or loss percentage in this transaction. (If it is needed, round your answer to the nearest hundredths)
Solution :
Total amount spent on the house is
= 49,000 + 6,000 + 5,000
= 60,000
This is the cost price of the house ($60,000).
Selling price of the house = $58,000
Because the selling price of the house is less than the cost price, there is loss.
Finding Loss :
Loss = Cost price - Selling price
Loss = 60,000 - 58,000
Loss = 2,000
Finding Loss Percentage :
Loss % = (Loss/Cost price) ⋅ 100 %
Loss % = (2000/60000) ⋅ 100 %
Loss % = 3.33 %
Problem 3 :
Goods are purchased for $1500. If one fifth of the goods sold at a profit of 5% and the remaining four-fifth of the goods at a profit of 10%, find the net profit percentage.
Solution :
Cost price of one-fifth of the goods is
= 1/5 ⋅ 1500
= 300
Selling price of one-fifth of the goods (at 5% profit) is
= (100 + 5)% of 300
= 105% of 300
= 1.05 ⋅ 300
= 315
Cost price of remaining four-fifth of the goods is
= 4/5 ⋅ 1500
= 1,200
Selling price of the remaining four-fifth of the goods (at 10% profit) is
= (100 + 10)% of 1200
= 110% of 1200
= 1.10 ⋅ 1200
= 1,320
Selling price of the total goods
= 315 + 1,320
= 1,635
Finding Net Profit :
Net profit = S.P of total goods - C.P of total goods
Net Profit = 1635 - 1500
Net Profit = 135
Finding Net Profit Percentage :
Net profit % = (Net profit/Cost price) ⋅ 100 %
Net profit % = (135/1500) ⋅ 100 %
Net profit % = 9 %
Problem 4 :
A trader bought a product for $200. If marks his goods 20% above the cost price and gives a discount of 10% for cash, find his profit percentage
Solution :
Cost price of the product = $100
Marked price (20% above the cost price) is
= (100 + 20) % of 200
= 120% of 200
= 1.2 ⋅ 200
= 240
Selling price price is the price which is after 20% discount from the marked price.
So, the selling price is
= (100 - 10) % of Marked price
= 90% of 240
= 0.9 ⋅ 240
= 216
Finding Profit :
Profit = Selling price - Cost price
Profit = 216 - 200
Profit = 16
Finding Profit Percentage :
Profit % = (Profit/Cost price) ⋅ 100 %
Profit % = (16/200) ⋅ 100 %
Profit % = 8 %
Problem 5 :
A person wants to get 20% profit after selling his object at 20% discount. Find the required percentage increase in marked price.
Solution :
Let the cost price be $100.
Then, the selling price (at 20% profit) is
= (100 + 20)% of 100
= 120% of 100
= 1.2 ⋅ 100
= 120
Selling price is the price which is after 20% discount from the marked price.
It has been illustrated in the picture given below.
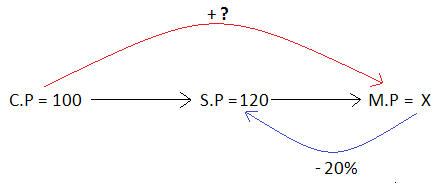
From the above picture, we get
Selling price = (100 - 20)% of Mmarked price
120 = 80% of x
120 = 0.8 ⋅ x
Divide both sides by 0.8
120/0.8 = x
1200/8 = x
150 = x
So, the marked price is $150.
Here,
Cost price = $100
Marked Price = $150
Hence, the required percentage increase is 50%
To learn profit and loss shortcuts,
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Volume of Cone Questions and Answers
Jan 18, 21 11:58 AM
Volume of Cone Questions and Answers
-
Volume of Cylinder Questions and Answers
Jan 18, 21 11:13 AM
Volume of Cylinder Questions and Answers
-
Examples on Volume of Cylinder
Jan 18, 21 10:20 AM
Examples on Volume of Cylinder
