VOLUME OF PYRAMID

Pyramid is basically a prism where all the side walls will be triangles and there will be no top portion.

To understand, how to find volume of a pyramid, let us consider the pyramid given below.

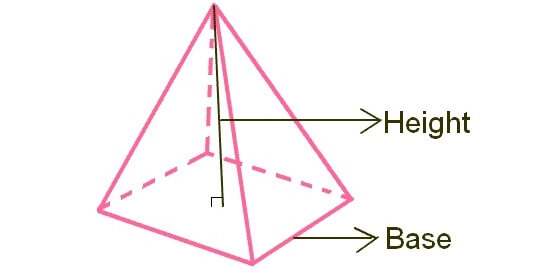
Formula to find volume of the above pyramid

= (1/3) x Base area x Height

Find the volume of the pyramid :

Example 1 :

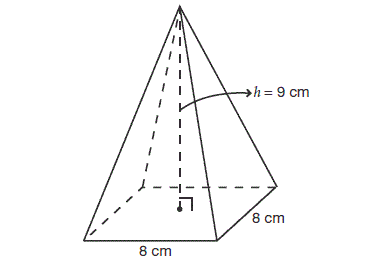
Solution :

Formula to find volume of pyramid is

=  (1/3) x Base area x Height

Here, the base is a square with side length 8 cm. 

So, area of the base is 

=  8 x 8

=  64 cm²

Height of the pyramid is 9 cm.

Then, volume of the pyramid is 

=  (1/3) x 64 x 9

=  192 cm³

Example 2 :

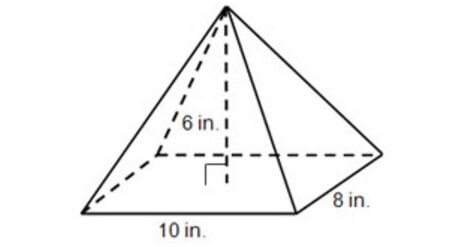
Solution :

Formula to find volume of pyramid is

=  (1/3) x Base area x Height

Here, the base is a rectangle with side length 10 inches and width 8 inches.  

So, area of the base is

=  10 x 8

=  80 in²

Height of the pyramid is 6 inches.

Then, volume of the pyramid is

=  (1/3) x 80 x 6

=  160 in³

Example 3 :

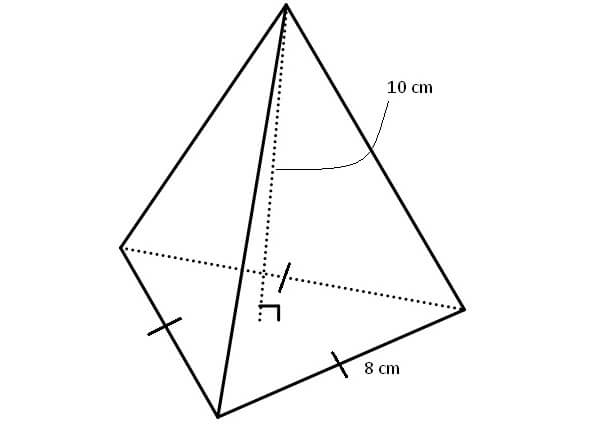
Solution :

Formula to find volume of pyramid is

=  (1/3) x Base area x Height

Here, the base is an equilateral triangle with side length of 8 cm.

So, area of the base is

=  (√3 / 4) x 8²

=  16√3 cm²

Height of the pyramid is 10 cm.

Then, volume of the pyramid  is

=  (1/3) x (16√3) x 10

=  160√3 / 3 cm³

Example 4 :

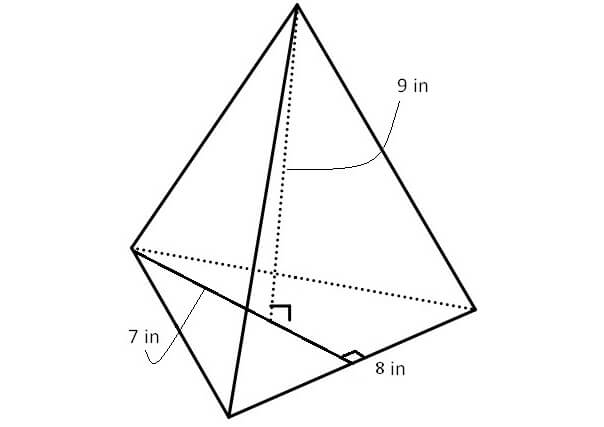
Solution :

Formula to find volume of pyramid is

=  (1/3) x Base area x Height

Here, the base is a triangle with height 7 inches and base 8 inches.

So, area of the base is 

=  (1/2) x 8 x 7

=  28 in²

Height of the pyramid is 9 inches.

Then, volume of the pyramid is 

=  (1/3) x 28 x 9

=  84 in³

Example 5 :

A pyramid has a volume of 40 cubic feet and a height of 6 feet. Find one possible set of dimensions of the rectangular base.

Solution :

Volume of pyramid = 40 cubic feet

height = 6 feet

base area x height = 40

(1/3) area of rectangular base x 6 = 40

Area of rectangular base = (40/6) x 3

= 20

length x width = 20

One of length and width :

length = 4 feet and width = 5 feet

Example 6 :

Originally, Khafre’s Pyramid had a height of about 144 meters and a volume of about 2, 218, 800 cubic meters. Find the side length of the square base.

Solution :

Volume of pyramid = area of square base x height

height = 144 meters

(1/3) area of base x 144 = 2, 218, 800 cubic meters.

(1/3) area of base = 2, 218, 800/144

Area of square base = 46225

Let side length be s

s² = 46225

s = √46225

= 215

So, the side of the square is 215 meters.

Example 7 :

Pyramid A and pyramid B are similar. Find the volume of pyramid B.

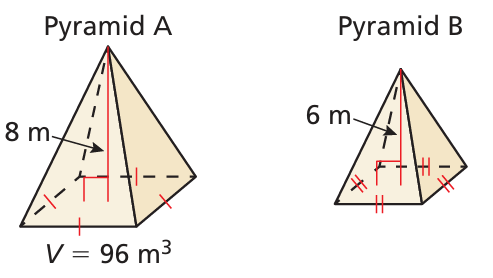
Solution :

Volume of pyramid A = 96 m³

Volume of pyramid A / volume of pyramid B = (Ratio of corresponding sides)³

96/volume of pyramid B = (8/6)³

96/volume of pyramid B = 512 / 216

96 x (216/512) = Volume of pyramid B

Volume of pyramid B = 40.5 cubic meter

Example 8 :

Pyramid C and pyramid D are similar. Find the volume of pyramid D.

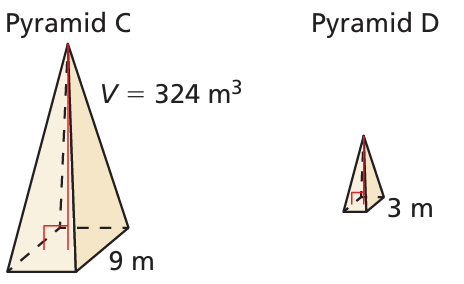
Solution :

Volume of pyramid A = 324 m³

Volume of pyramid A / volume of pyramid B = (Ratio of corresponding sides)³

324/volume of pyramid B = (9/3)³

324/volume of pyramid B = 3³

Volume of pyramid B = 324/27

= 12

Volume of pyramid B = 12 cubic meter

Example 9 :

Find the volume of the composite solid

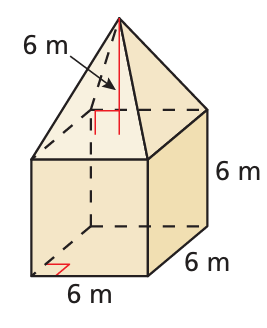
Solution :

Volume of composite figure = volume of cube + volume of square base pyramid

Let s be the side length of cube. 

= s³ + (1/3) x base area x height

= 6³ + (1/3) x 6 x 6 x 6

= 216 + 216/3

= 216 + 72

= 288 m³

So, the volume of composite figure is 288 m³.

Example 10 :

A pyramid with a rectangular base has a volume of 105 cubic centimeters and a height of 15 centimeters. The length of the rectangular base is 7 centimeters. Find the width of the rectangular base.

Solution :

Volume of rectangular base pyramid

= (1/3) x base area x height

= (1/3) x length x width x height

length of base = 7 cm, height = 15 cm abd volume = 105 cubic cm

(1/3) x 7 x width x 15 = 105

Width = (105 x 3)/(7 x 15)

= 315/105

= 3 cm

So, the width of the rectangular base is 3 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.