TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES

Two acute angles are complementary to each other if their sum is equal to 90°. In a right triangle the sum of the two acute angles is equal to 90°. So, the two acute angles of a right triangle are always complementary to each other.

Let ABC be a right triangle, right angled at B.  

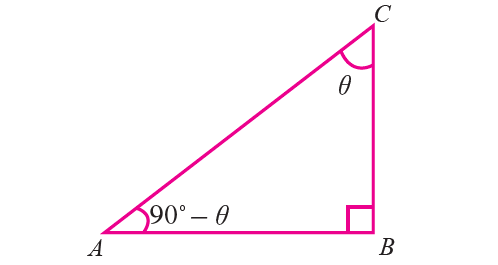
If  ∠ACB = θ, then  ∠BAC = 90° - θ and hence the angles  ∠BAC and  ∠ACB are complementary

For the angle θ, we have 

Similarly, for the angle (90° - θ), we have

Comparing the equations in (1) and (2) we get,

sin θ  =  AB/AC  =  cos (90 - θ)

cos θ  =  BC/AC  =  sin (90 - θ)

tan θ  =  AB/BC  =  cot (90 - θ)

cosec θ  =  AC/AB  =  sec (90 - θ)

sec θ  =  AC/BC  =  cosec (90 - θ)

cot θ  =  BC/AB  =  tan (90 - θ)

Practice Questions

Question 1 :

Evaluate

cos 56° / sin 34°

Answer : 

The angles 56° and 34° are complementary.

Use trigonometric ratios of complementary angles. 

cos 56° / sin 34°  =  cos 56° / cos (90° - 34°)

cos 56° / sin 34°  =  cos 56° / cos 56°

cos 56° / sin 34°  =  1

Question 2 :

Evaluate 

tan 25° / cot 65°

Answer : 

The angles 25° and 65° are complementary.

Use trigonometric ratios of complementary angles.

tan 25° / cot 65°  =  tan 25) / tan (90° - 65°)

tan 25° / cot 65°  =  tan 25° / tan 25°

tan 25° / cot 65°  =  1

Question 3 :

Evaluate 

(cos 65° sin 18° cos 58°)/(cos 72° sin 25° sin 32°)

Answer : 

Use trigonometric ratios of complementary angles.

cos 65°  =  cos (90° - 25°)  =  sin 25°

sin 18°  =  sin (90° - 72°)  =  cos 72°

cos 58°  =  cos (90° - 32°)  =  sin 32°

(cos 65° sin 18° cos 58°) / (cos 72° sin 25° sin 32°) is

=  (sin 25° cos 72° sin 32°) / (cos 72° sin 25° sin 32°)

=  1

So, 

cos 65° sin 18° cos 58°)/(cos 72° sin 25° sin 32°  =  1

Question 4 :

Evaluate :

tan 35° tan 60° tan 55° tan 30°

Answer : 

tan 35°  =  tan (90° - 55°)  =  cot 55°  =  1/tan 55°

tan 60°  =  tan (90° - 30°)  =  cot 30°  =  1/tan 30°

tan 35° tan 60° tan 55° tan 30° :  

=  (1/tan 55° ) x (1/tan 30°) tan 55° tan 30° 

=  1

So, 

tan 35° tan 60° tan 55° tan 30°   =  1

Question 5 :

If sin A  =  cos 33°, find A.

Answer : 

sin A  =  cos 33°

sin A  =  sin (90° - 33°) 

  sin A  =  sin 57°

A  =  57°

Question 6 :

If tan A tan 35°  =  1, find A.

Answer : 

tan A tan 35°  =  1

Divide  each side by tan 35°. 

tan A  =  1/tan 35°

tan A  =  cot 35°

tan A  =  tan (90° - 35°)

tan A  =  tan 55°

A  =  55°

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.