TRANSLATING WORD PROBLEMS INTO EQUATIONS

Translating a sentence or statement into an algebraic equation is an important stuff which is much required to solve word problems in math. 

Let us see, how to translate the information given in a word problem into an algebraic expression or equation in the following examples. 

Example 1 :

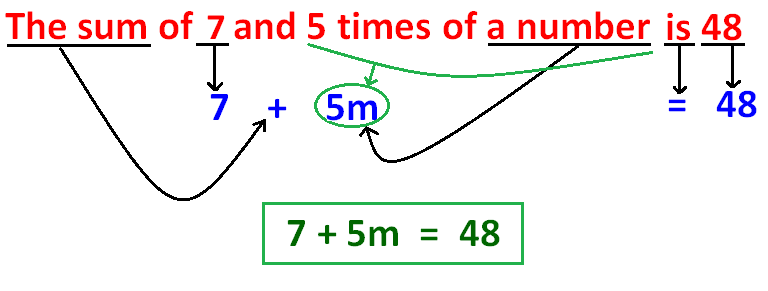
Example 2 :

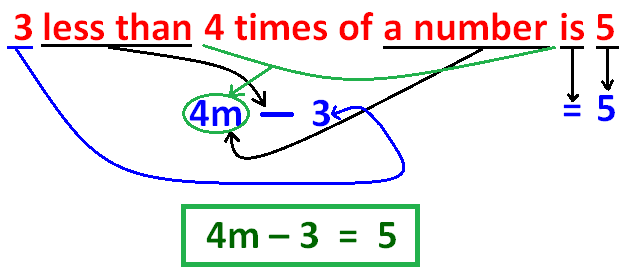
Example 3 :

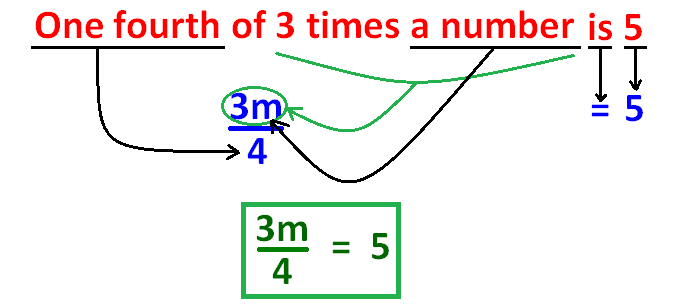
Example 4 :

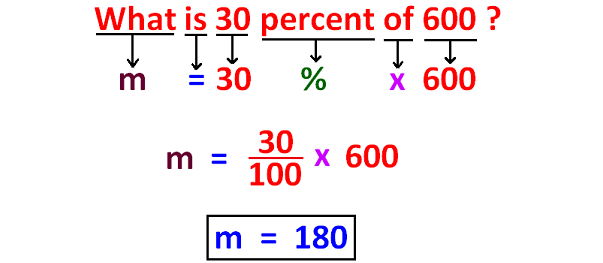
Example 5 :

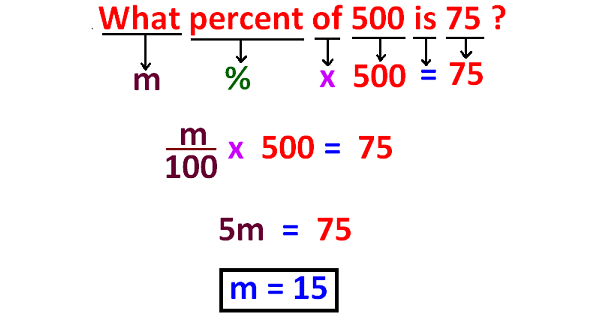
Translating Word Problems into Equations Step by Step

Problem :

The age of a father is thrice the sum of the ages of his two sons and 5 years hence his age will be twice the sum of their ages. Find the present age of the father.

Solution :

Step 1 :

Let us understand the information given.

There are two information given in the question. 

1. The age of the father is thrice the sum of the ages of his two sons. (At present)

2. After 5 years, his age would be twice the sum of their ages. (After 5 years)

Step 2 :

Target of the question : Present age of the father

Step 3 :

Introduce required variables for the information given in the question. 

Let x be the present age of the father.

Let y be the sum of present ages of two sons.

Clearly, the value of x to be found.

Because that is the target of the question.

Step 4 :

Translate the given information as mathematical equation using x and y. 

First information :  

The age of the father is thrice the sum of the ages of his two sons.

Translation (i) :

The Age of the father ----->  x

is ----->  =

Thrice the sum of the ages of his two sons ----->  3y 

Equation related to the first information using x and y is

x  =  3y -----(1)

Second Information :

After 5 years, his age would be twice the sum of their ages.

Translation (ii) :

Age of the father after 5 years ----->  (x + 5)

After 5 years :

Sum of the ages of his two sons ----->  y + 5 + 5  =  y + 10

(Here we have added 5 two times.The reason is there are two sons)

Twice the sum of ages of two sons -----> 2(y + 10)

would be ----->  =

Equations related to the second information using x and y is

x + 5  =  2(y + 10)

Simplify.

x + 5  =  2y + 20

Subtract 2y and 5 from each side.

x - 2y  =  15 -----(2)

Step 5 :

Solve (1) and (2) to find the value of the unknown.

Substitute 3y for x in (2).

(2)-----> 3y - 2y  =  15

y  =  15

Substitute 15 for y in (1).

(1)-----> x  =  3(15)

x  =  45

Therefore, the present age of the father is 45 years.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.