SPECIAL LINE SEGMENTS IN TRIANGLES WORKSHEET

Problem 1 :

In the triangle ABC, angle A is divided in to equal halves by the line segment AC. What type of line segment is AC ?

Problem 2 :

In the triangle ABC, the line segment AD is passing through the vertex A and also perpendicular to the opposite side of the vertex A. What type of line segment is AD ?

Problem 3 :

In the triangle ABC, the line segment ED is not passing through any of the vertex but it is perpendicular to one of the sides of the triangle and also passing through the mid point of the same side. What type of line segment is ED ? 

Problem 4 :

In the triangle ABC, the line segment AD is passing through the vertex A, perpendicular to the side BC and also passing through the mid point of the side BC. What type of line segment is AD ? 

Problem 5 :

In the triangle ABC, the line segment AD joining the vertex A and the midpoint of the side BC.  What type of line segment is AD ? 

Problem 6 :

In the triangle ABC, there is a angle bisector at angle A. After the angle A is divided in to two equal halves, if each half measures 22°, find angle A.

Problem 7 :

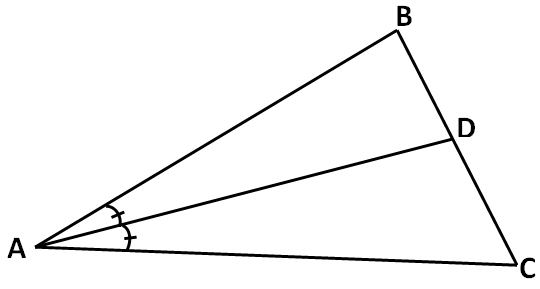
In the triangle given below, AD is the angle bisector. If ∠B  =  70° and ∠C  =  60°, find ∠BAD and ∠DAC. 

Problem 8 :

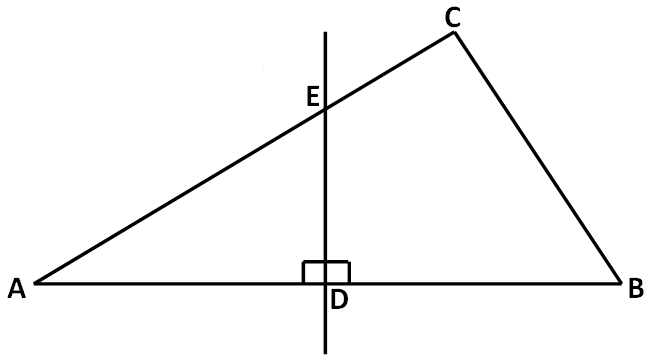
In the triangle given below, ED is the perpendicular bisector. If ∠B  =  60° and ∠C  =  70°, find angle ∠AED. 

Problem 9 :

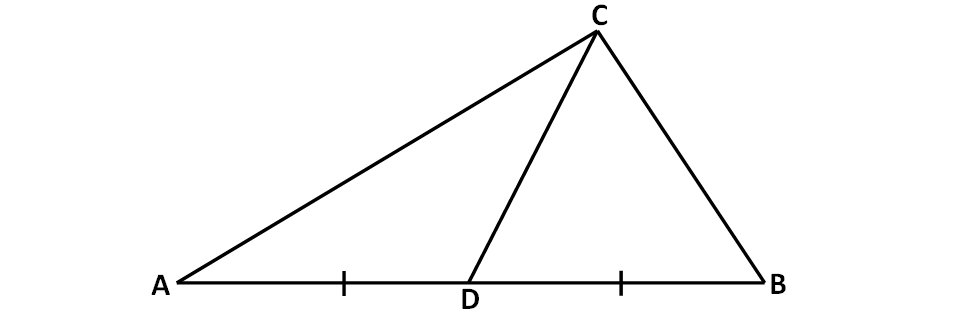
In the triangle given below, CD is the median. If ∠B  = 60° and ∠ADC  =  120°, find ∠BCD.

Problem 10 :

In the triangle given below, AD  =  4 cm and BC  =  8 cm, find the area of the triangle. 

Detailed Answer Key

Problem 1 :

In the triangle ABC, angle A is divided in to equal halves by the line segment AC. What type of line segment is AC ?

Solution : 

Given :  Angle A is divided in to equal halves by the line segment AC.

Only the angle bisector will divide an angle in to equal halves.

So, the line segment AC is angle bisector.

Problem 2 :

In the triangle ABC, the line segment AD is passing through the vertex A and also perpendicular to the opposite side of the vertex A. What type of line segment is AD ?

Solution : 

Given : The line segment AD is passing through the vertex A and also perpendicular to the opposite side of the vertex A.

Only the altitude will pass through the vertex and perpendicular to the opposite side of the vertex. 

So, the line segment AD is altitude.

Problem 3 :

In the triangle ABC, the line segment ED is not passing through any of the vertex but it is perpendicular to one of the sides of the triangle and also passing through the mid point of the same side. What type of line segment is ED ? 

Solution : 

Given : The line segment ED is not passing through any of the vertex but it is perpendicular to one of the sides of the triangle and also passing through the mid point of the same side

Since the line segment ED is not passing through any of the vertex, it can not be altitude.

But ED is perpendicular to one of the sides of the triangle and also it is passing through the midpoint of the same side. 

So, the line segment ED is perpendicular bisector.

Problem 4 :

In the triangle ABC, the line segment AD is passing through the vertex A, perpendicular to the side BC and also passing through the mid point of the side BC. What type of line segment is AD ? 

Solution : 

Given : The line segment AD is passing through the vertex A, perpendicular to the side BC and also passing through the mid point of the side BC

Since the line segment AD is passing through one of the vertices vertex and perpendicular to the side BC, clearly AD is altitude. 

But AD is also passing through the midpoint of BC. So it is also perpendicular bisector and median. 

So, the line segment AD is altitude,  perpendicular bisector and median.

Problem 5 :

In the triangle ABC, the line segment AD joining the vertex A and the midpoint of the side BC.  What type of line segment is AD ? 

Solution : 

Given : The line segment AD joining the vertex A and the midpoint of the side BC. 

Only the median will join one of the vertices of the triangle and the mid point of the opposite side of the vertex.

So, the line segment AD is median.

Problem 6 :

In the triangle ABC, there is a angle bisector at angle A. After the angle A is divided in to two equal halves, if each half measures 22°, find angle A.

Solution :

Given : Angle A is divided in to two equal halves by the angle bisector and each half measures 22°, 

Angle A  =  22° + 22°

Angle A  =  44°

Problem 7 :

In the triangle given below, AD is the angle bisector. If ∠B  =  70° and ∠C  =  60°, find ∠BAD and ∠DAC. 

Solution :

The angle sum property of a triangle states that the angles of a triangle always add up to 180°.

Then, 

∠A + ∠B + ∠C  =  180°

∠A + 70° + 60°  =  180°

∠A + 130°  =  180°

∠A  =  50°

Because AD is the angle bisector, it divides the angle ∠A into two equal halves. That is 25° and 25°

So, 

∠BAD  =  25°

∠DAC  =  25°

Problem 8 :

In the triangle given below, ED is the perpendicular bisector. If ∠B  =  60° and ∠C  =  70°, find angle ∠AED. 

Solution :

The angle sum property of a triangle states that the angles of a triangle always add up to 180°.

∠A + ∠B + ∠C  =  180°

∠A + 60 + 70  =  180

∠A + 130  =  180

∠A  =  50°

In triangle AED, we have

∠A + ∠AED + ∠EDA  =  180°

50 + ∠AED + 90  =  180

∠AED + 140  =  180

∠AED  =  40°

Problem 9 :

In the triangle given below, CD is the median. If ∠B  = 60° and ∠ADC  =  120°, find ∠BCD.

Solution :

Given :  ∠ADC  =  120°

From the given figure, angle ADC and angle CDB together form a straight angle.

Then, 

∠ADC + ∠CDB  =  180°

120° + ∠CDB  =  180°

∠CDB  =  60°

In triangle BCD, we have 

∠B + ∠BCD + ∠CDB  =  180°

60° + ∠BCD + 60°  =  180°

∠BCD + 120°  =  180°

∠BCD  =  60°

Problem 10 :

In the triangle given below, AD  =  4 cm and BC  =  8 cm, find the area of the triangle. 

Solution : 

In the given figure, clearly AD is the height (altitude) and BC is the base of the triangle. 

Area of the triangle  =  (1/2) ⋅ b ⋅ h

=  (1/2) ⋅ 8 ⋅ 4

=  16 square cm.

So, the area of the triangle is 16 square cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.