SIMPLE INTEREST PROBLEMS

Problem 1 :

Find the simple interest on $6,900 at 16⅔% per year for 2 years.

Solution :

Formula for simple interest is

I = Prt

Here, P = 6900, n = 2, r = 16⅔% = 50/3%.

Substitute these values in the above formula.

I = 6900 ⋅ (50/3) / 100 ⋅ 2

= 6900 ⋅ 50/300 ⋅ 2

= 2300

Hence, the interest earned is $240.

Problem 2 :

If a sum of money is doubled in 10 years in simple interest, in how many years will it be tripled?

Solution :

Let P be the sum of money.

Given : P is doubled in 10 years.

Now we can calculate interest for ten years as given below.

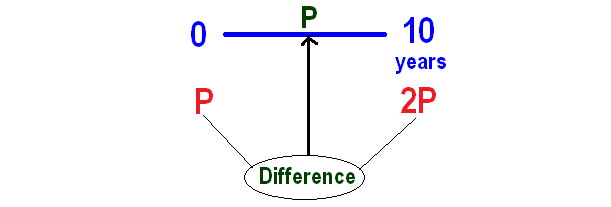
From the above calculation, P is the interest for the first 10 years.

In simple interest, interest earned will be same for every year.

Interest earned in the next 10 years will also be P.

It has been explained below.

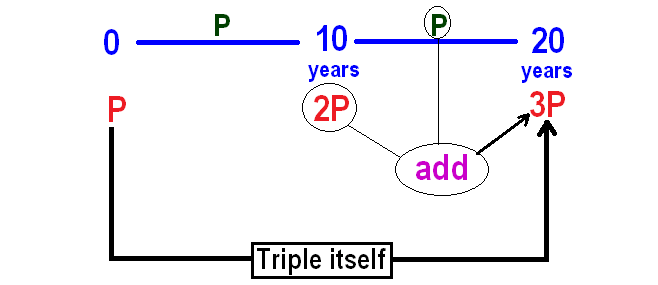
Hence, the sum of money will be tripled in 20 years.

Problem 3 :

If a sum of money amounts to $ 6200 in 2 years and $ 7400 in 3 years under simple interest, then find the principal.

Solution :

From the given given information we have the following points.

At the end of 2 years, we get $6200

At the end of 3 years, we get $7400

From the above two points,  we can get the interest earned in the 3rd year.

It has been explained below.

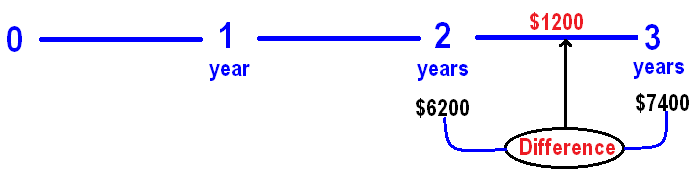
In simple interest, interest will be same for every year.

So, we can calculate the principal as given below.

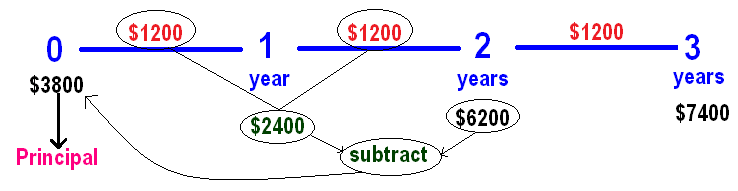
Hence, the principal is $3800.

Problem 4 :

If a sum of money produces $3900 as interest in 3 years and 3 months at 16% per year simple interest, find the principal.

Solution :

Formula for simple interest is

I = Prt ----(1)

Here, I = $3900, r = 16%, P = ?

The value of "t" must always be in "years". But in the question, it is given in both years and months.

To convert months into years, we have to divide the given months by 12.

Then, we have

t = 3 years 3 months

= 3 3/12  years

= 3¼ years

= 13/4 years

Substitute I = 3900, r = 16/100 and t = 13/4 in (1).

3900 = P ⋅ 16/100 ⋅ 13/4

3900 = P ⋅ 13/25

Multiply both sides by 25/13.

3900 ⋅ 25/13 = P

7500 = P

Hence, the required principal is $7500.

Problem 5 :

Arthur invests his inheritance of $24,000 in two different accounts which pay 6% and 5% annual interest. After one year, he received $1330 in interest. How much did he invest in each account?

Solution :

Let x be the amount invested in 6% account.

Then, the amount invested in 5% account is

= 24000 - x

Given : Total interest earned on both the accounts is $1340.

So, we have

Interest in 6% account + Interest in 5% account = 1330.

x ⋅ 6/100 ⋅ 1 + (24000 - x) ⋅ 5/100 ⋅ 1 = 1330

0.06x + (24000 - x)0.05 = 1330

0.06x + 1200 - 0.05x = 1330

0.01x + 1200 = 1330

Subtract 1200 from both sides.

0.01x  =  130

Divide both sides by 0.01.

x = 130/0.01

x = 13000

And also,

24000 - x = 24000 - 13000

24000 - x = 11000

Hence, the amount invested in 6% account is $13,000 and in 5% account is $11,000.

Problem 6 :

Mr. Garret invested twice as much money at 6% as he did at 7%. After one year, his earnings at 6% were $95 more than his earnings at 7%. Find the amount invested at each rate.

Solution :

Let x be the amount invested at 7% rate.

Then, the amount invested in 6% rate is

= 2x

Interest earned after 1 year at 7% rate is

= x ⋅ 7/100 ⋅ 1

= 0.07x ----(1)

Interest earned after 1 year at 6% rate is

= 2x ⋅ 6/100 ⋅ 1

= 0.12x ----(2)

Given : Earnings at 6% were $95 more than his earnings at 7%.

That is, earnings in (2) were $95 more than the earnings in (1).

So, we have

(2) - (1) = 95

0.12x - 0.007x = 95

0.05x = 95

Divide both sides by 0.05

x = 95/0.05

x = 9500/5

x = 1900

And also,

2x = 2 ⋅ 1900

2x = 3800

Hence, the amount invested at 7% rate $1900 and at 6% rate is $3800.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.