SECTION FORMULA

Let A and B be two towns. Assume that one can reach town B from A by moving 60 km towards east and then 30 km towards north. A telephone company wants to raise a relay tower at P which divides the line joining A and B in the ratio 1 : 2 internally.

Now, it wants to find the position of P where the relay tower is to be set up. Choose the point A as the origin. Let P(x, y) be the point. Draw the perpendiculars from P and B to the x-axis, meeting it in C and D respectively. Also draw a perpendicular from P to BD, intersecting at E.

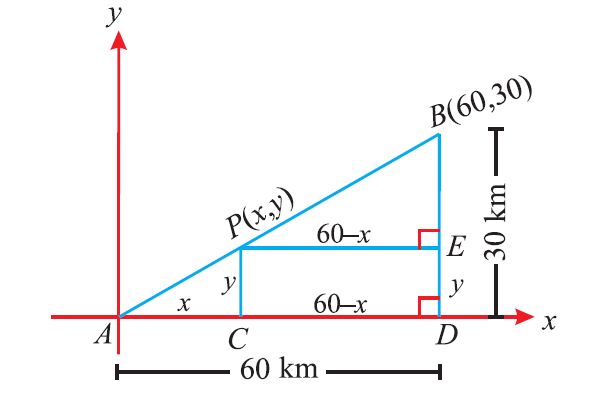
Since ΔPAC and ΔBPE are similar, we have

Therefore, the position of the relay tower is at P(20, 10).

Taking the above problem as a model, we shall derive the general section formula.

Let A(x₁, y₁) and B(x₂, y₂) be two distinct points such that a point P(x, y) divides AB internally in the ratio l : m.

That is,

AP/PB = l/m

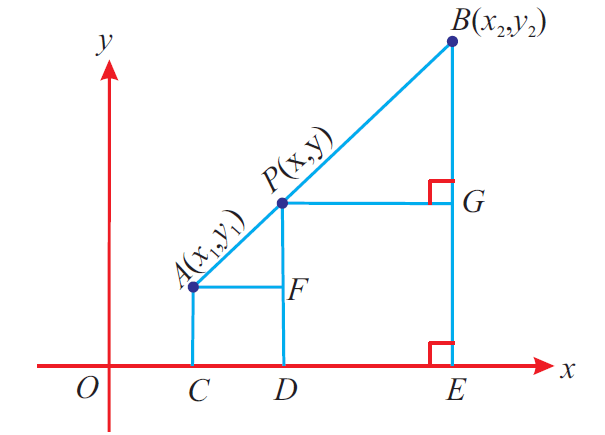
From the diagram above, we get

AF = CD = OD - DC = x - x₁

PG = DE = OE - OD = x₂ - x

Also,

PF = PD - FD = y - y₁

BG = BE - GE = y₂ - y

Now, ΔAFP and ΔPGB are similar.

Thus

Thus, the point P which divides the line segment joining the two points A(x₁, y₁) and B(x₂, y₂) internally in the ratio l : m is

This formula is known as section formula.

It is clear that the section formula can be used only when the related three points are collinear.

Results

Let AB be a line segment joining the two points A(x₁, y₁) and B(x₂, y₂) externally in the ratio l : m, then the point P is :

Solved Problems

Problem 1 :

Find the point which divides the line segment joining the points (3 , 5) and (8 , 10) internally in the ratio 2 : 3.

Solution :

Let A(3, 5) and B(8, 10) be the given points.

Let the point P(x, y) divide the line AB internally in the ratio 2 : 3.

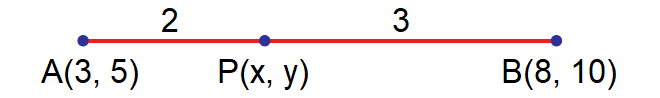
By section formula,

Here (x₁, y₁) = (3, 5), (x₂, y₂) = (8, 10), l = 2 and m = 3.

Problem 2 :

In what ratio does the point P(-2, 3) divide the line segment joining the points A(-3, 5) and B(4, -9) internally?

Solution :

Given points are A(-3, 5) and B(4, -9).

Let P (-2, 3) divide AB internally in the ratio l : m.

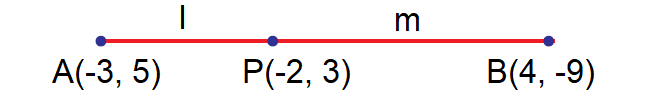
By the section formula,

Here (x₁, y₁) = (-3, 5) and (x₂, y₂) = (4, -9).

Equating the x-coordinates, we get

Hence P divides AB internally in the ratio 1 : 6.

Problem 3 :

Find the points of trisection of the line segment joining

(4, -1) and (-2, -3)

Solution :

Let A(4, -1) and B(-2, -3) be the given points.

Let P(x, y) and Q(a, b) be the points of trisection of AB so that

AP = PQ = QB

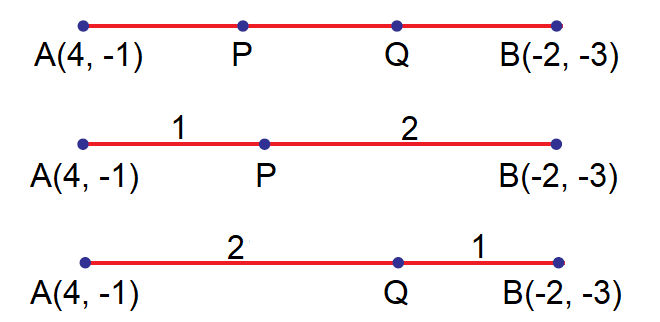
Hence P divides AB internally in the ratio 1 : 2 and Q divides AB internally in the ratio 2 : 1.

By the section formula, the required points are

Note that Q is the midpoint of PB and P is the midpoint of AQ.

Problem 4 :

Find the coordinates of the point which divides the line segment joining (3, 4) and (–6, 2) in the ratio 3 : 2 externally.

Solution :

Let A(3, 4) and B(-6, 2) be the given points.

Let the point P(x, y) divide the line AB externally in the ratio 3 : 2.

By section formula,

Here (x₁, y₁) = (3, 4), (x₂, y₂) = (-6, 2), l = 3 and m = 2.

Problem 5 :

Find the points which divide the line segment joining (-4, 0) and (0, 6) into four equal parts.

Solution :

Let A(-4, 0) and B(0, 6) be the given points.

Let P, Q and R be the three points which divide the line AB into four equal parts.

P divides the line segment in the ratio 1 : 3.

By section formula, point P :

Q divides the line segment in the ratio 2 : 2.

By section formula, point Q :

R divides the line segment in the ratio 3 : 1.

By section formula, point R :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.