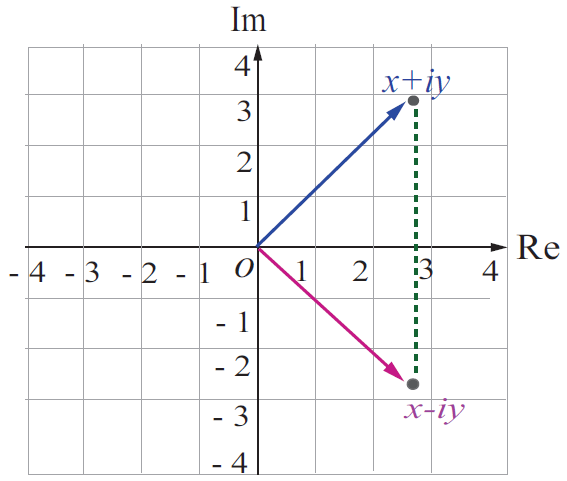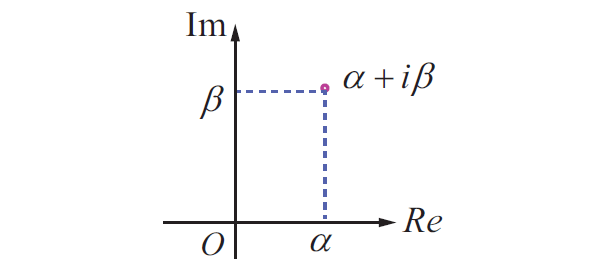SECTION FORMULA WORKSHEET
Question 1 :
Using the section formula, show that the points
A(1, 0),B (5, 3), C (2, 7) and D(-2, 4)
are vertices of a parallelogram taken in order.
Question 2 :
The 4 vertices of a parallelogram are
A(-2, 3), B(3, -1), C(p, q) and D(-1, 9)
Find the value of p and q.
Question 3 :
Find the coordinates of the point which divides the line segment joining
(3, 4) and (-6, 2)
in the ratio 3:2 externally.
Question 4 :
Find the coordinates of the point which divides the line segment joining (-3, 5) and (4, -9) in the ratio 1:6 internally.
Question 5 :
Let A (-6 , -5) and B(-6 , 4) be the two points such that a point P on the line AB satisfies AP = (2/9) AB. Find the point P.
Question 6 :
Find the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4).
Question 7 :
Find the ratio in which x axis divides the line segment joining the points (6, 4) and (1,- 7).
Question 8 :
Find the ratio in which x axis divides the line segment joining the points (6 , 4) and (1 ,- 7).
Question 9 :
Find the coordinates of the points of trisection of the line segment joining the points A(−5, 6) and B(4,−3).
Question 10 :
The line segment joining A(6,3) and B(−1, −4) is doubled in length by adding half of AB to each end. Find the coordinates of the new end points.
Question 11 :
Find the points which divide the line segment joining A(-4, 0) and B(0, 6) into four equal parts
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
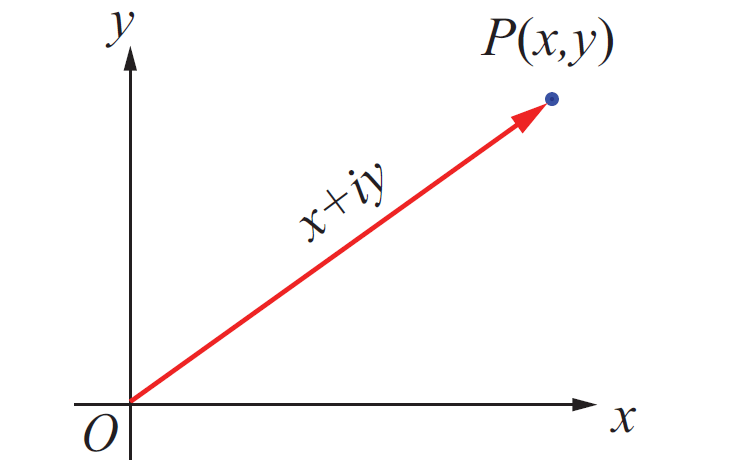
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane