ROTATION TRANSFORMATION MATRIX

Rotation transformation matrix is the matrix which can be used to make rotation transformation of a figure.

We can use the following matrices to find the image after 90°, 180°, 270° clockwise and  counterclockwise rotation.

Rule

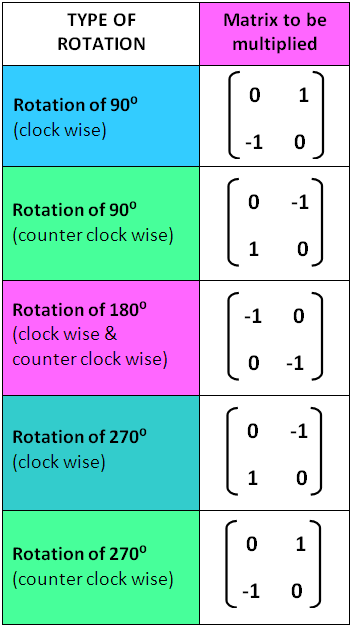
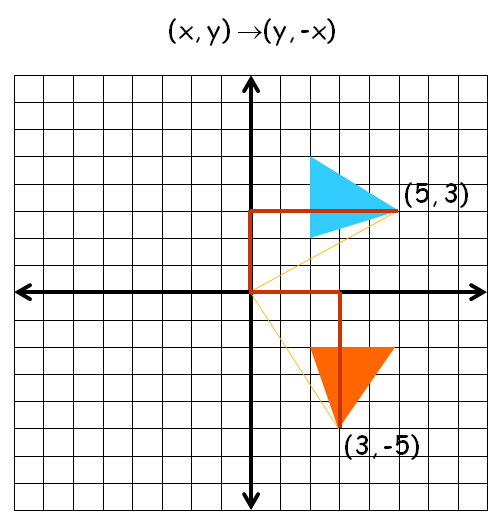
90° Rotation (Clock Wise)

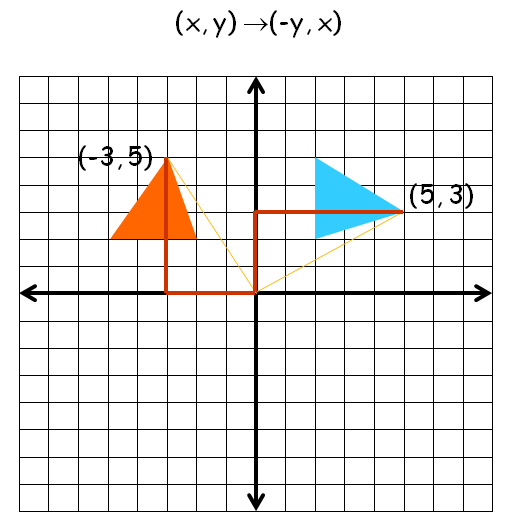
90° Rotation (Counter Clock Wise)

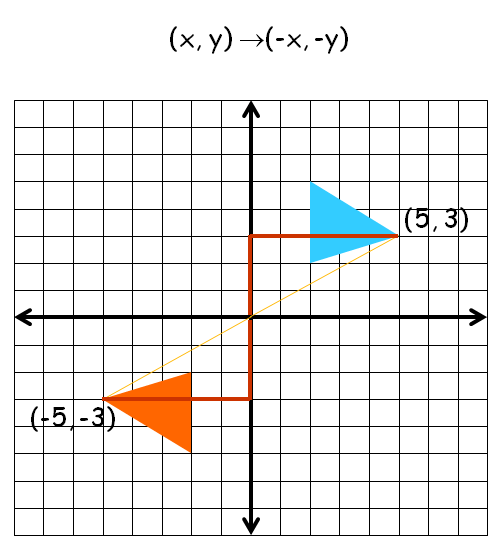
180° Rotation (Clock Wise and Counter Clock Wise)

Once students understand the rules which they have to apply for rotation transformation, they can easily make rotation  transformation of a figure.

Let us consider the following example to have better understanding of rotation transformation using matrices.

Question :

Let A (-2, 1), B (2, 4) and (4, 2) be the three vertices of a triangle. If this triangle is rotated about 90° counter clockwise, find the vertices of the rotated image A'B'C' using matrices.

Solution :

Step 1 :

First we have to write the vertices of the given triangle ABC  in matrix form as given below.

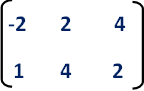
Step 2 :

Since the triangle ABC is rotated about 90° counter clockwise, to get the rotated image, we have to multiply the above matrix by  the matrix given below.

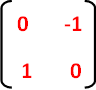
Step 3 :

Now, let us multiply the two matrices.

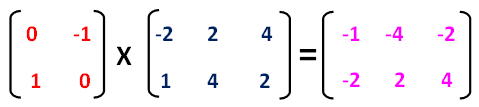
Step 4 :

Now we  can get vertices of the rotated image A'B'C' from the resultant matrix.

Vertices of the reflected image are

A'(-1, -2), B'(-4 , 2) and C'(-2 , 4)

How to sketch the rotated figure ?

1. First we have to plot the vertices of the pre-image.

2. In the above problem, the vertices of the pre-image are

A(-2, 1), B(2, 4) and C(4 , 2)

3. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure).

4. When we rotate the given figure about 90° counter clock wise,  vertices of the image are

A'(-1 , -2) , B'(-4 , 2) and C'(-2 , 4)

7. When plot these points on the graph paper, we will get the figure of the image (rotated figure).

Solved Problems

Problem 1 :

Let K (-4, -4), L (0, -4), M (0, -2) and N(-4, -2) be the vertices of a rectangle. If this rectangle is rotated 90° clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

K'(-4, 4), L'(-4, 0), M'(-2, 0) and N'(-2, 4)

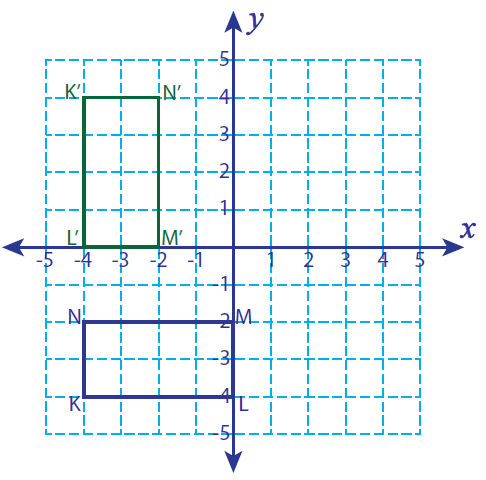
Problem 2 :

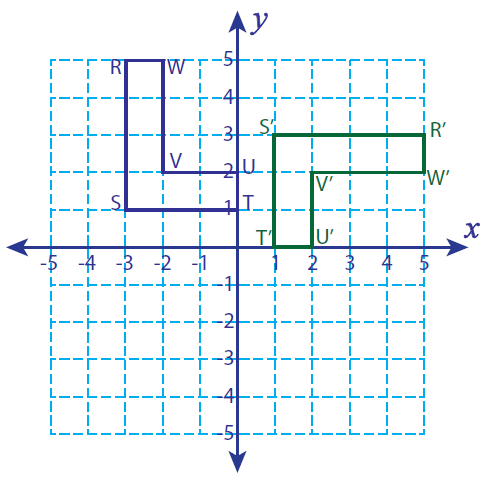
Let R (-3, 5), S (-3, 1), T (0, 1), U (0, 2), V (-2, 2) and W (-2, 5) be the vertices of a closed figure. If this figure is rotated 90° clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

R'(5, 3), S'(1, 3), T'(1, 0), U'(2, 0), V'(2, 2) and W'(5, 2)

Problem 3 :

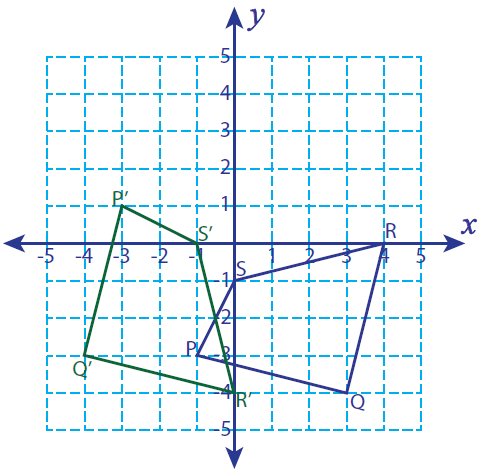
Let P (-1, -3), Q (3, -4), R (4, 0) and S (0, -1) be the vertices of a closed figure. If the figure is rotated 90° clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

P'(-3, 1), Q'(-4, -3), R(0, -4) and S'(-1, 0)

Problem 4 :

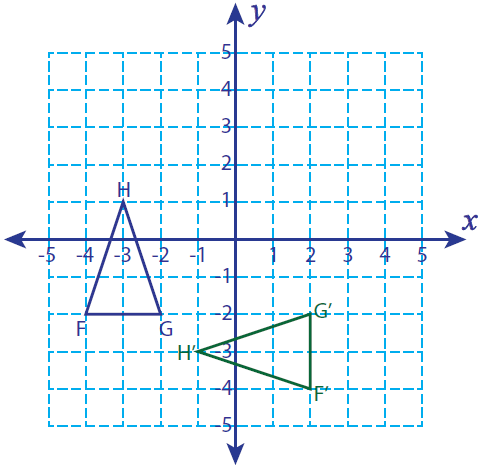
Let F (-4, -2), G (-2, -2) and H (-3, 1) be the three vertices of a triangle. If this triangle is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

F'(2, -4), G'(2, -2) and H'(-1, -3)

Problem 5 :

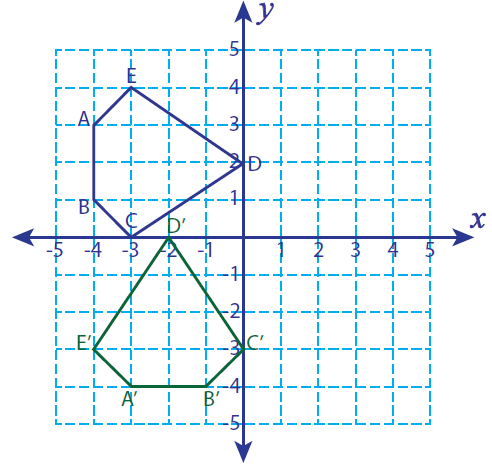
Let A (-4, 3), B (-4, 1), C (-3, 0), D (0, 2) and E (-3,4) be the vertices of a closed figure. If this figure is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

A'(-3, -4), B'(-1, -4), C'(0, -3), D'(-2, 0) and E'(-4, -3)

Problem 6 :

Let D (-1, 2), E (-5, -1) and F (1, -1) be the vertices of a triangle. If the triangle is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

D'(-2, -1), E'(1, -5) and F'(1, 1)

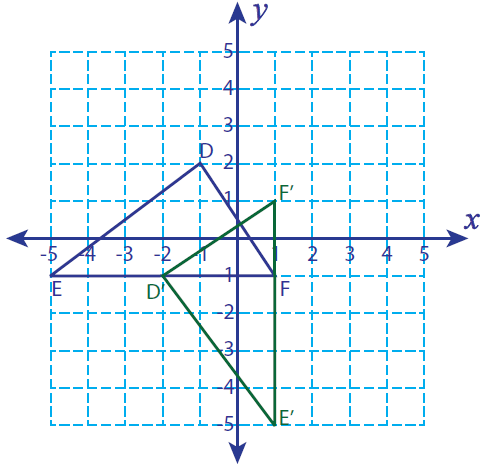
Problem 7 :

Let P (-2, -2), Q (1, -2) R (2, -4) and S (-3, -4) be the vertices of a four sided closed figure. If this figure is rotated 180° clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

P'(2, 2), Q'(-1, 2), R'(-2, 4) and S'(3, 4)

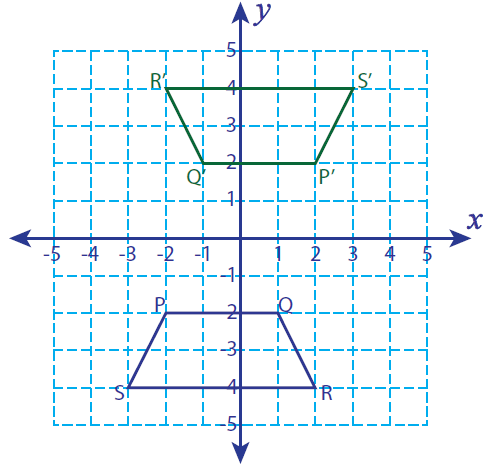
Problem 8 :

Let K (1, 4), L (-1, 2), M (1, -2) and N (3, 2) be the vertices of a four sided closed figure. If this figure is rotated 180° counter clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

K'(-1, -4), L'(1, -2), M'(-1, 2) and N'(-3, -2)

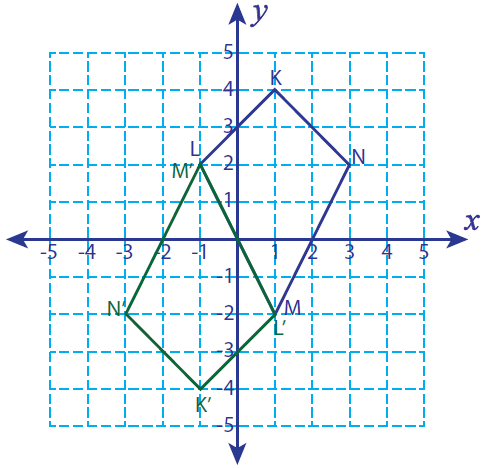
Problem 9 :

Let T (1, -3), U (5, -5), V (3, -3) and W (5, -1) be the vertices of a closed figure. If this figure is rotated 270° counter clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

T'(-3, -1), U'(-5, -5), V'(-3, -3) and  W'(-1, -5)

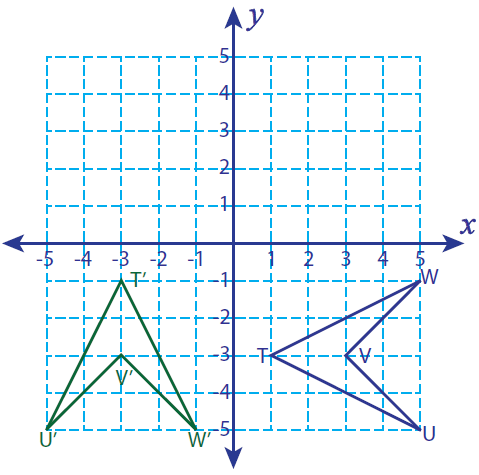
Problem 10 :

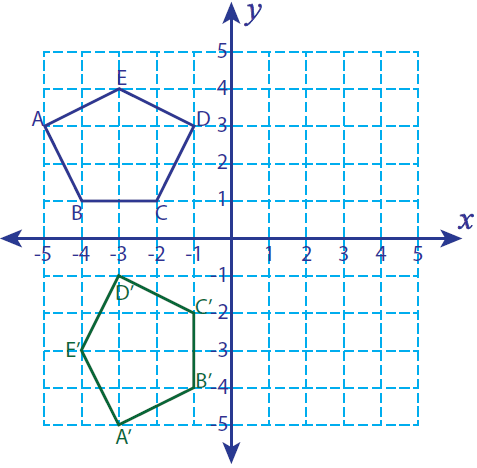
Let A (-5, 3), B (-4, 1), C (-2, 1) D (-1, 3) and E (-3,  4) be the vertices of a closed figure. If this figure is rotated 270° clockwise, find the vertices of the rotated figure and graph.

Solution :

Vertices of the rotated figure are

A'(-3, -5), B'(-1, -4), C'(-1, -2), D'(-3, -1) and E'(-4, -3)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.