SUM AND PRODUCT OF ROOTS OF QUADRATIC EQUATION

If a quadratic equation is given in standard form, we can find the sum and product of the roots using coefficient of x², x and constant term. 

Let us consider the standard form of a quadratic equation,  

ax² + bx + c  =  0

(Here a, b and c are real and rational numbers)

Let α and β be the two zeros of the above quadratic equation. 

Then the formula to get sum and product of the roots of a quadratic equation is,

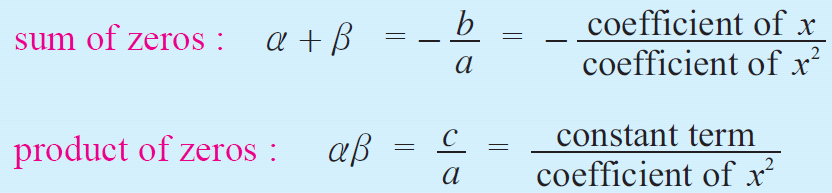
Example 1 :

Find the sum and product of roots of the quadratic equation given below.

x² - 5x + 6  =  0

Solution :

Comparing

x² - 5x + 6  =  0

and 

ax² + bx + c  =  0

we get

a  =  1, b  =  -5 and c  =  6

Therefore, 

Sum of the roots  =  -b/a  =  -(-5)/1  =  5

Product of the roots  =  c/a  =  6/1  =  6

Example 2 :

Find the sum and product of roots of the quadratic equation given below.

x² - 6  =  0

Solution :

Comparing

x² - 6  =  0

and 

ax² + bx + c  =  0

we get

a  =  1, b  =  0 and c  =  -6

Therefore, 

Sum of the roots  =  -b/a  =  0/1  =  0

Product of the roots  =  c/a  =  -6/1  =  -6

Example 3 :

Find the sum and product of roots of the quadratic equation given below. 

3x² + x + 1  =  0

Solution :

Comparing

3x² + x + 1  =  0

and 

ax² + bx + c  =  0

we get

a  =  3, b  =  1 and c  =  1

Therefore, 

Sum of the roots  =  -b/a  =  -1/3

Product of the roots  =  c/a  =  1/3

Example 4 :

Find the sum and product of roots of the quadratic equation given below.

3x² + 7x  =  2x - 5

Solution :

First write the given quadratic equation in standard form.

3x² +7x  =  2x - 5

3x² + 5x + 5  =  0

Comparing

3x² + 5x + 5  =  0

and 

ax² + bx + c  =  0

we get

a  =  3, b  =  5 and c  =  5

Therefore, 

Sum of the roots  =  -b/a  =  -5/3

Product of the roots  =  c/a  =  5/3

Example 5 :

Find the sum and product of roots of the quadratic equation given below.

3x² -7x + 6  =  6

Solution :

First write the given quadratic equation in standard form.

3x² -7x + 6  =  6

3x² - 7x  =  0

Comparing

3x² - 7x  =  0

and 

ax² + bx + c  =  0

we get

a  =  3, b  =  -7 and c  =  0

Therefore, 

Sum of the roots  =  -b/a  =  -(-7)/3  =  7/3

Product of the roots  =  c/a  =  0/3  =  0

Example 6 :

Find the sum and product of roots of the quadratic equation given below.

x² + 5x + 1  =  3x² + 6

Solution :

First write the given quadratic equation in standard form.

x² + 5x + 1  =  3x² + 6

0  =  2x² - 5x + 5

2x² - 5x + 5  =  0

Comparing

2x² - 5x + 5  =  0

and 

ax² + bx + c  =  0

we get

a  =  2, b  =  -5 and c  =  5

Therefore, 

Sum of the roots  =  -b/a  =  -(-5)/3  =  5/2

Product of the roots  =  c/a  =  5/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.