RELATIONS AND FUNCTIONS

Relations :

Relation is nothing but connecting the elements of one set to another set which is called as mapping.

The connection of elements from one set to another set will be written as ordered pairs. 

Let us consider the mapping of elements from set A to set B. 

Let a ∈ A and b ∈ B, then the relation "R" from A to B can be defined as follows.

R  =  { (a, b) }

Important Note : 

Here, relation R is defined from A to B. In case, the relation is defined from B to A, each ordered pair of the relation set will be (b, a)

Most importantly, (a, b) ≠ (b, a)

Mapping from A to B and B to A are completely different.

So, mapping from A to B and B to A are two different relations and they are inverse to each other. 

Functions :

Function is also a relation, but the relation has to fulfill some conditions, if it wants to be a function. 

The two important conditions for a relation to be as a function. 

Let the mapping be done from the set A to set B. 

(i) Each element of A has to be involved in mapping.

(ii) Each element of A has to be mapped to at most one element in B.   

In other words, 

(i) Each element of A must have an image in B.

(ii) Each element of A must have an unique image (not more than one image) in B. 

If either of the above conditions is not met, then the relation is not a function.

There fore, 

All the functions are relations. But all the relations need not be functions.

If a relation wants to be as a function, it has to meet the above two conditions. 

Other important terms related to relations and functions.

If a relation does mapping from the set A to set B, then we can define the following terms. 

Domain : Set A

Co domain : Set B

Range : Elements of B involved in mapping

Example :

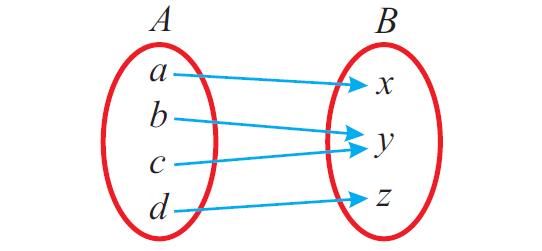
In the above mapping from A to B, each element of A has an image in B. And also, each element of A unique image (not more than one image) in B. 

Since, the above given relation meets both the conditions, it is a function. 

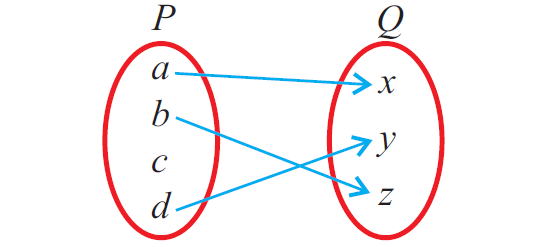
In the above mapping from P to Q, the element "c" in P does not have image in Q. 

Since, the above given relation does not meet the first condition, it is not a function.

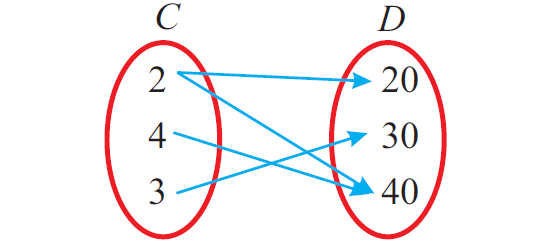
In the above mapping from C to D, each element of C has an image in D. 

But, the element 2 in C has two images (20, 40) in D, it does not meet the second condition. So, it is not a function.

Representation of Functions

A function can be represented in the following four ways. 

(i)  A set of ordered pairs :

Let f : A ---> B

The set f  =  { (a , b) /  a ∈ A and b ∈ B } of all ordered pairs represents the function

(ii)  A table :

The elements of A and their respective images under f can be given in the form of a table.

(iii)  An arrow diagram :

An arrow diagram indicates the elements of the domain of f and their respective images by means of arrows.

(iv)  A graph :

The ordered pairs in the collection f are plotted as points (x, y) in the x-y plane. The graph of f is the totality of all such points.

Example : 

Let A  =  { 0, 1, 2, 3 } and B  =  { 1, 3, 5, 7, 9 } be two sets.        Let f : A ---> B be a function given by f (x)  =  2x + 1. Represent this function as (i) a set of ordered pairs (ii) a table (iii) an arrow diagram and (iv) a graph.

Solution :

(i)  A set of ordered pairs :

Here x ----> elements of A  and  f(x) ----> elements of B

Then, we have 

f(0)  =  2(0) + 1  =  0 + 1  =  1 -------> (0, 1) 

f(1)  =  2(1) + 1  =  2 + 1  =  3 -------> (1, 3)

f(2)  =  2(2) + 1  =  4 + 1  =  5 -------> (2, 5)

f(3)  =  2(3) + 1  =  6 + 1  =  7-------> (3, 7)

The given function f can be represented as a set of ordered pairs as

f  =  { (0, 1), (1, 3), (2, 5), (3, 7) }

(ii)  A table :

Let us represent f using a table as shown below.

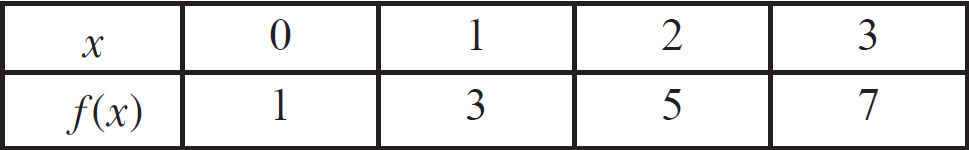
(iii)  An arrow diagram :

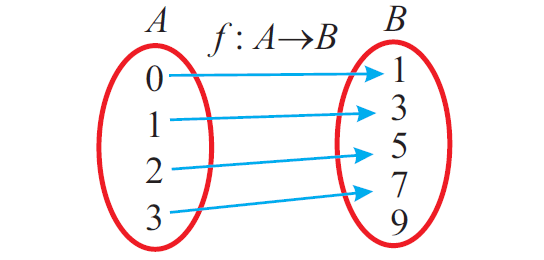
(iv)  A graph :

If the order pairs are written as points in the form (x, y), we will get the points (0, 1), (1, 3), (2, 5) and (3, 7).

These points are plotted on the x-y plane as shown below.

The totality of all points represent the graph of the function.

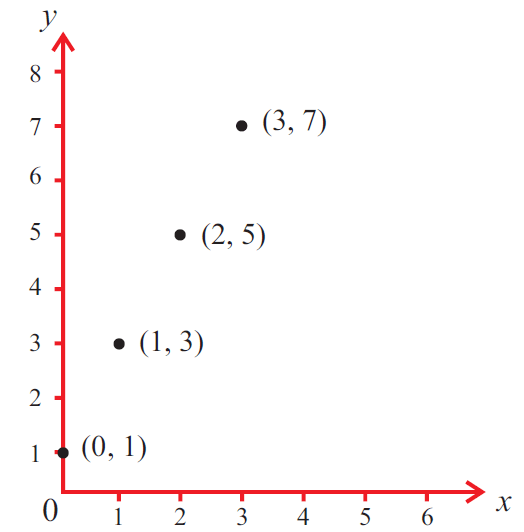
Vertical Line Test

Here, we are going to see, whether the given graph represents a function or not. 

Key Concept :

A graph represents a function only if every vertical line intersects the graph in at most one point.

Example 1 :

Use the vertical line test to determine whether the following graph represents a function.

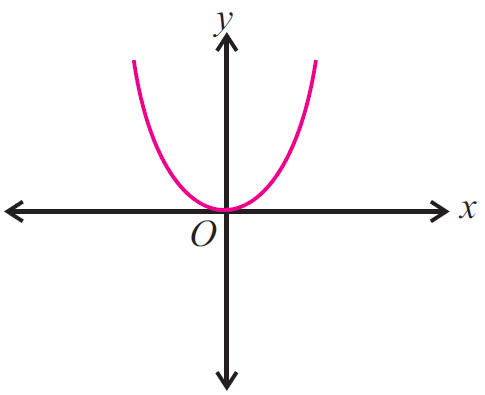
Solution :

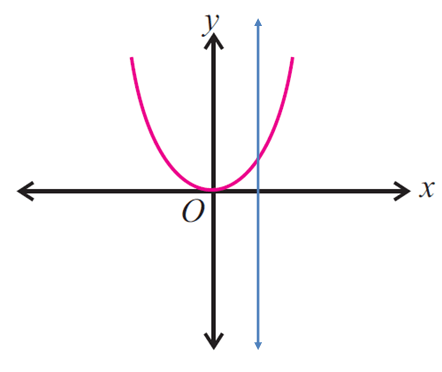
Since the vertical line intersects the graph in at most one point, the given  graph represents a function. 

Example 2 :

Use the vertical line test to determine whether the following graph represents a function.

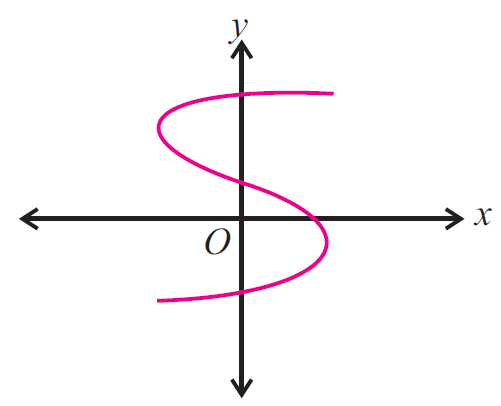
Solution :

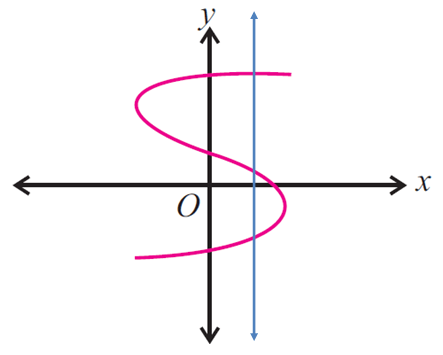
Since the vertical line intersects the graph in more than one point (three points), the given  graph does not represent a function. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.