RATE OF CHANGE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Rate of change is generally expressed as a ratio between a change in one variable relative to a corresponding change in another variable.
Graphically, the rate of change is represented by the slope of a line.
Change in y-value/change in x-value
Determining Rate of Change and Initial Value
Example 1 :
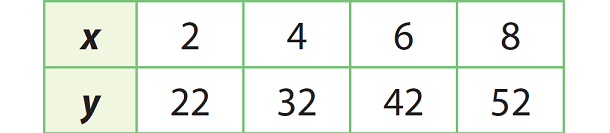
What is the rate-of-change between 6 and 8?
Solution :
Rate of change = Change in y-value/change in x-value
Change in y - value from 6 and 8 = 42 - 52 = -10.
Change in x - value from 6 and 8 = 6 - 8 = -2.
Rate of change :
= -10/(-2)
= 5
Example 2 :
A phone salesperson is paid a minimum weekly salary and a commission for each phone sold, as shown below. Find the rate of change between 20 and 40.
No. of phones sold
10
20
30
40
Weekly income ($)
$480
$630
$780
$930
Solution :
Rate of change = Change in y-value/change in x-value
Change in y - value from 20 and 40 = 630 - 930 = -300
Change in x - value from 20 and 40 = 20 - 40 = -20
Rate of change :
= -300/(-20)
= 15
Example 3 :
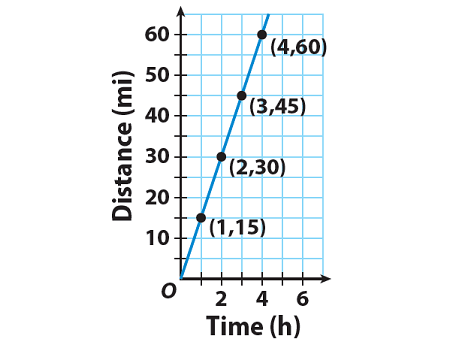
The graph shows the distance Nathan bicycled over time. What is Nathan’s rate of change between 1 hour to 4 hours?
Solution :
Rate of change = Change in y-value/change in x-value
Change in y - value from 1 hour to 4 hours = 15 - 45 = -30
Change in x - value from 1 hour to 4 hours = 20 - 40 = -20
Rate of change :
= -300/(-20)
= 15
Constant Rate of Change
Constant rate is also called as uniform rate which involves something travelling at fixed and steady pace or else moving at some average speed.
Example 4 :
David drove for 3 hours at a rate of 50 miles per hour, for 2 hours at 60 miles per hour and for 4 hours at a rate of 70 miles per hour. What was his constant-speed for the whole journey?
Solution :
Step 1 :
Formula for constant speed :
= Total distance/Total time taken
Formula for distance :
= Rate x Time
Step 2 :
Distance covered in the first 3 hours :
= 50 x 3
= 150 miles
Distance covered in the next 2 hours :
= 60 x 2
= 120 miles
Distance covered in the last 4 hours :
= 70 x 5
= 350 miles
Step 3 :
Total distance :
= 150 + 120 + 350
= 620 miles
Total time :
= 3 + 2 + 5
= 10 hours
Step 4 :
So, constant speed :
= 620/10
= 62 miles per hour
So, the constant speed for the whole journey is 62 miles per hour.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 1)
Feb 05, 26 09:37 AM
Digital SAT Math Problems and Solutions (Part - 1) -
AP Precalculus Problems and Solutions
Feb 05, 26 06:41 AM
AP Precalculus Problems and Solutions -
SAT Math Preparation with Hard Questions
Feb 05, 26 05:30 AM
SAT Math Preparation with Hard Questions

