APPLICATION PROBLEMS OF RATE OF CHANGE IN CALCULUS
Problem 1 :
Newton's law of cooling is given by θ = θ₀° e⁻kt, where the excess of temperature at zero time is θ₀° C and at time t seconds is θ° C. Determine the rate of change of temperature after 40 s given that θ₀ = 16° C and k = -0.03.(e1.2 = 3.3201)
Solution :
Newton's law of cooling θ = θ₀° e⁻kt
θ₀° = 16° C
k = -0.03
rate of change of temperature with respect to time
dθ/dt = - k θ₀° e^(⁻kt)
t = 40
dθ/dt = - (-0.03) (16)e^(⁻0.03) (40)
= 0.48 e⁻1.2
= 0.48 (3.3201)
= 1.5936° C/s
Problem 2 :
The altitude of a triangle is increasing at a rate of 1 cm/min while the area of the triangle is increasing at a rate of 2 cm²/min. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 100 cm².
Solution :
Let "b" and "h" be the base and height of the triangle ABC.
Area of triangle ABC
A = (1/2) b h
h = 10 area = 100
100 = (1/2) x b x 10
b = (100 x 2)/10
b = 20
dA/dt = (1/2) [b (dh/dt) + h (db/dt)]
h (db/dt) = 2 (dA/dt) - b (dh/dt)
db/dt = (2/h) (dA/dt) - (b/h) (dh/dt)
db/dt = (2/10) (2) - (20/10) (1)
db/dt = (4/10) - (20/10)
db/dt = -16/10
db/dt = -1.6 cm/min
Problem 3 :
At noon, ship A is 100 km west of ship B. Ship A is sailing east at 35 km/hr and ship B us sailing north at 25 km/hr. How fast is the distance between the ship changing at 4.00 p.m
Solution :
Let P and Q are the starting position of the ships A and B.
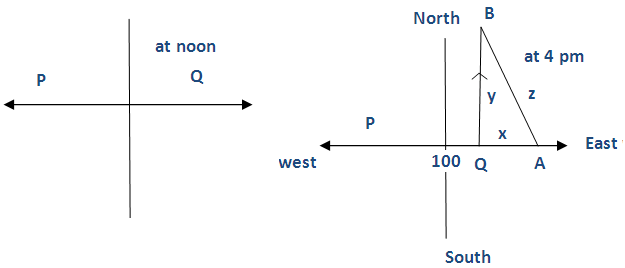
Let x, y and z be the distance between QA and QB and AB respectively.
z2 = x2 + y2
Here x, y and z are changing with respect to time.
2z (dz/dt) = 2x (dx/dt) + 2y (dy/dt)
Dividing each side by 2.
z (dz/dt) = x (dx/dt) + y (dy/dt)
dx/dt = speed of ship A = 35 km/hr
dy/dt = speed of B = 25 km/hr
x = 40, y = 100
z = √(40)2 + (100)2
z = √1600 + 10000
z = √2600
z = 20√29
20√29 (dz/dt) = 40 (35) + (100) (25)
20√29 (dz/dt) = 1400 + 2500
20√29 (dz/dt) = 3900
dz/dt = 3900 /(20√29)
dz/dt = 195/√29
There the rate of change of distance between two ships is 195/√29 km/hr.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Printable Math Worksheets
Apr 20, 24 12:02 AM
Printable Math Worksheets - Worksheets in Pdf formats from grade 1 to 10 -
Printable Math Worksheets for Grade 2
Apr 19, 24 11:58 PM
Printable Math Worksheets for Grade 2 -
Sequences and Series
Apr 19, 24 11:45 PM
Sequences and Series - Concept - Examples