HOW TO FIND THE RANK OF 3X3 MATRIX
To define rank, we require the notions of submatrix and minor of a matrix.
A matrix obtained by leaving some rows and columns from the matrix A is called a submatrix of A. In particular A itself is a submatrix of A, because it is obtained from A by leaving no rows or columns.
The determinant of any square submatrix of the given matrix A is called a minor of A.
If the square submatrix is of order r, then the minor is also said to be of order r.
Find Rank of Matrix by Minor Method
(i) If a matrix contains at least one non zero element, then ρ (A) ≥ 1
(ii) The rank of the identity matrix In is n.
(iii) If the rank of a matrix A is r, then there exists at-least one minor of A of order r which does not vanish and every minor of A of order r + 1 and higher order (if any) vanishes.
(iv) If A is an m × n matrix, then
ρ(A) ≤ min {m, n} = minimum of m, n.
(v) A square matrix A of order n has inverse
if and only if ρ(A) = n.
Find Rank of Matrix by Echelon Form
(i) The first element of every non zero row is 1.
(ii) The row which is having every element zero should be below the non zero row.
(iii) Number of zeroes in the next non zero row should be more than the number of zeroes in the previous non zero row.
By elementary operations one can easily bring the given matrix to the echelon form.
Finding Rank Minor Method
Example :
Find the rank of the matrix.
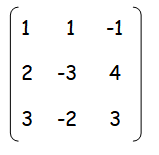
Solution :

|A| = 1(-9+8)-1(6-6)-1(-4+9)
= 1(-1)-1(0)-1(5)
= -1-5
|A| = -6 ≠ 0
Since the given matrix in non singular matrix, it has inverse. ρ(A) = 2.
Finding Rank Echelon Form
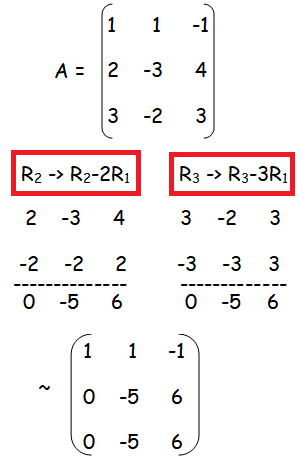
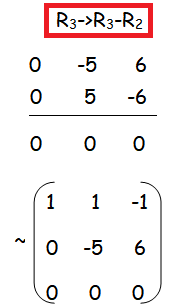
Number of non zero rows are 2, so ρ(A) = 2.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number