SOLVING WORD PROBLEMS INVOLVING THE SHAPES SQUARES AND RECTANGLES
Problem 1 :
The side of a square exceeds the side of another square by 4
cm and the sum of the area of two squares is 400 sq.cm. Find the dimensions of
the squares.
Solution :
Let x be side length of one square
The side of a square exceeds the side of another square by 4 cm
So, the side length of another square = x + 4
Area of one square with side length x = x2
Area of one square with side length x + 4 is (x + 4)²
Sum of the area of two squares = 400 sq.cm
x2 + (x + 4)2 = 400
x2 + x2 + 2 ⋅ x ⋅ 4 + 42 = 400
2x2 + 8x + 16 - 400 = 0
2x2 + 8x - 384 = 0
By dividing the entire equation by 2, we get
x2 + 4x - 192 = 0
(x + 16) (x - 12) = 0
|
x + 16 = 0 x = -16 |
x - 12 = 0 x = 12 |
Therefore sides of one square is 12 cm.
Side length of another square = (12 + 4) = 16 cm.
Problem 2 :
The length of the rectangle exceeds its width by 2 cm and the area of the rectangle is 195 sq.cm. Find the dimensions of the rectangle.
Solution :
Let x and y be the width and length of rectangle respectively
The length of the rectangle exceeds its width by 2 cm
So, length (y) = x + 2
Area of the rectangle = 195 sq.cm
Length ⋅ width = 195
x⋅(x + 2) = 195
x2 + 2x - 195 = 0
(x + 15) (x - 13) = 0
|
x + 15 = 0 x = -15 |
x - 13 = 0 x = 13 |
Here x represents width of the rectangle. So, the negative value is not possible.
To find the value of y we have to apply the value of x in the equation y = x + 2
y = 13 + 2
y = 15 cm
Therefore length of rectangle is 15 cm and width of the rectangle is 13 cm.
Problem 3 :
The footpath of uniform width runs all around a rectangular field 28 meters long and 22 meters wide. If the path occupies 600 m² area, find the width of the path.
Solution :
Let x be the width of the path
Length of the rectangular field = 28 m
Width of the rectangular field = 22 m
Area of the path = 600 m2
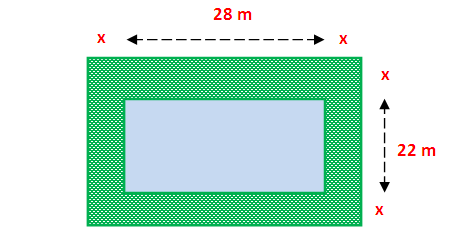
Length of the larger rectangle :
= 28 + x + x
= 28 + 2x
Width of the larger rectangle :
= 22 + x + x
= 22 + 2x
Area of the path = Area of larger rectangle - Area of smaller rectangle
600 = (28 + 2x) (22 + 2x) - 28 ⋅ 22
600 = 616 + 56x + 44x + 4x2 - 616
600 = 56x + 44x + 4x2
600 = 4x2 + 100 x
4x² + 100x = 600
Dividing the entire equation by 4, we get
x2 + 25x = 150
x² + 25x - 150 = 0
(x - 5) (x + 30) = 0
|
x - 5 = 0 x = 5 |
x + 30 = 0 x = -30 |
Negative value is not possible. Because x represents width of the path.
Therefore width of the path is 5 m

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
