PROOF OF PYTHAGOREAN THEOREM

To prove the Pythagorean theorem, let us consider the right triangle shown below.

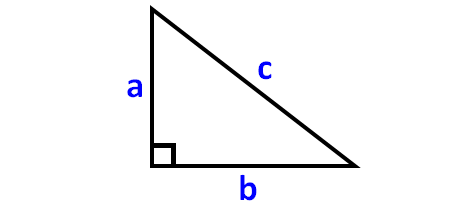
Now, let us annex a square on each side of the triangle as given below.

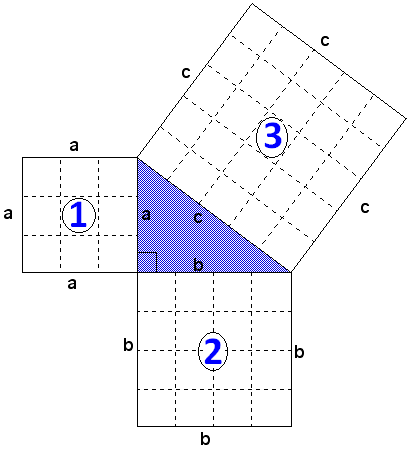
(Size of each small box in the squares 1, 2 and 3 are same in size)

In square 1, each side is divided into 3 units equally.

Then the side length of square 1, a = 3

In square 2, each side is divided into 4 units equally.

Then the side length of square 2, b = 4

In square 3, each side is divided into 5 units equally.

Then the side length of square 3, c = 5

Areas of Three Squares

Area of square 1 :

a² = 3² = 9 square units

Area of square 2 :

b² = 4² = 16 square units

Area of square 3 :

c² = 5² = 25 square units

In the areas of above three squares, we can have

Area of square 1 + Area of square 2 = Area of square 3

That is,

a² + b² = c²

From the above result, it is clear that the sum of squares of two sides of a right triangle is equal to the square of the third side.

Hence, Pythagorean theorem is proved.

Important points about right angle triangle :

1. The longest side is called as "hypotenuse"

2. In the above triangle "c" is hypotenuse.

3. The side which is opposite to right angle is hypotenuse.

4. Always the square of longest side (hypotenuse) is equal to the sum of the squares of other two sides.

5. If we know the lengths of two sides of a right angle triangle, we will be able to know the length of the third side using Pythagorean theorem.

Solving Problems Using Pythagorean Theorem

Problem 1 :

Find the value x in the given figure.

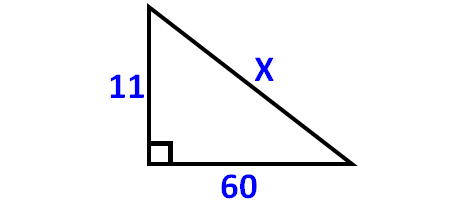
Solution :

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have,

60² + 11² = x²

3600 + 121 = x²

3721 = x²

61² = x²

61 = x²

So, the value of x is 61.

Problem 2 :

Find the value x in the given figure.

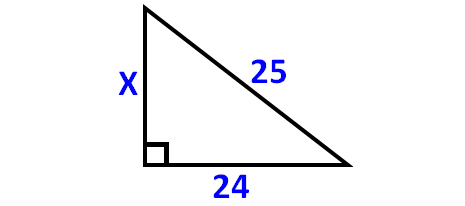
Solution :

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have,

x² + 24² = 25²

x² + 576 = 625

Subtract 576 from each side.

x² = 49

x² = 7²

x = 7

So, the value of x is 7.

Problem 3 :

If the height of a triangle is 17 inches less than the length of its base and the length of the hypotenuse is 25 inches, find the base and the height.

Solution :

Let x be the length of base.

Then, the height is (x - 17)

Given : Hypotenuse is 25 inches.

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have,

 x² + (x - 7)² = 25²

x² + x² - 2(x)(17) + 17² = 625 

2x² - 34x + 289 = 625

2x² - 34x - 336 = 0

x² - 17x - 168 = 0

(x + 7) (x - 24) = 0

x = -7  or  x = 24

Because the length of the side a triangle can never be a negative value, we can ignore x = -7.

Therefore, the value of x is 24.

Then,

x - 17 = 24 - 17

x - 17 = 7 inches

So, the base and height of the triangle are 24 and 7 inches respectively.

Problem 4 :

The sides of an equilateral triangle are shortened by 12 units, 13 units, 14 units respectively and a right angle triangle is formed. Find the length of side of the equilateral triangle.

Solution :

Let x be the length of side of the equilateral side.

Given : The sides of an equilateral triangle are shortened by 12 units, 13 units, 14 units and a right angle triangle is formed.

Then, new lengths of the triangle  are

(x - 12), (x - 13) and (x - 14)

These are the sides of a right angle triangle and (x - 12) is the longest side.

Because the longest side of the right triangle is hypotenuse, (x - 12) can be considered to be the length of the hypotenuse.

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have,

(x - 13)² + (x - 14)² = (x - 12)²

x² - 2(x)(13) + 13² + x² - 2(x)(14) + 14² = x² - 2(x)(12) + 144

x² - 26x + 169 + x² - 28x + 196 = x² - 24x + 144

2x² - 54x + 365 = x² - 24x + 144

 x² - 30x + 221 = 0

(x - 13)(x - 17) = 0

x = 13  or  x = 17

If we take x = 13, the sides of the right triangle are

x - 12 = 1

x - 13 = 0

x - 14 = -1

When x = 13, we get one of the sides is zero and the sign of the another side is negative.

Then, x = 13 can not be accepted.

If we take x = 17, the sides of the right triangle are

x - 12 = 5

x - 13 = 4

x - 14 = 3

All of the three sides of the right angle are positive when x = 17.

Moreover, the lengths 5, 4 and 3 satisfy the Pythagorean theorem.

That is,

5² = 4² + 3²

25 = 16 + 9

25 = 25

Therefore, x = 17 can be accepted.

So, the length of side of equilateral triangle is 17 units.

Problem 5 :

If the sum of the lengths of two sides of a right triangle is 49 inches and the hypotenuse is 41 inches, then find the two sides.

Solution :

Let x be one of the two sides.

Then the length of other side is (49 - x).

Given : Hypotenuse is 41 inches.

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have

x² + (49 - x)² = 41²

x² + 49² - 2(49)(x) + x² = 1681

2x² - 98x + 2401 = 1681

2x² - 98x + 720 = 0

x² - 49x + 360 = 0

(x - 40)(x - 9) = 0

x = 40  or  x = 9

If x = 40, then the length of other side is

= 49 - 40

= 9

If x = 9, then the length of other side is

= 49 - 9

= 40

So, the lengths of other two sides are 9 inches and 40 inches.

Problem 6 :

The foot of a ladder is placed 6 feet from a wall. If the top of the ladder rests 8 feet up on the wall, how long is the ladder?

Solution :

Draw a sketch.

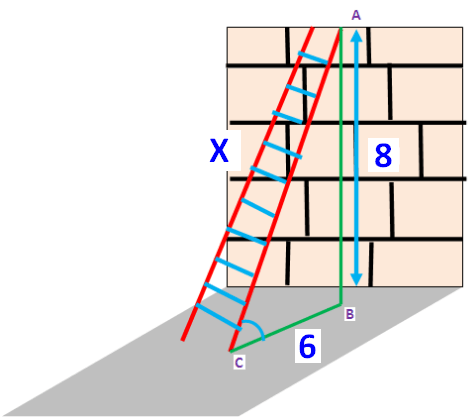
Let x be the required distance.

According to Pythagorean theorem, the square of the hypotenuse is equal to sum of the squares of other two sides.

Then, we have

8² + 6² = x²

64 + 36 = x²

100 = x²

10² = x²

10 = x

So, the length of the ladder is 10 feet.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.