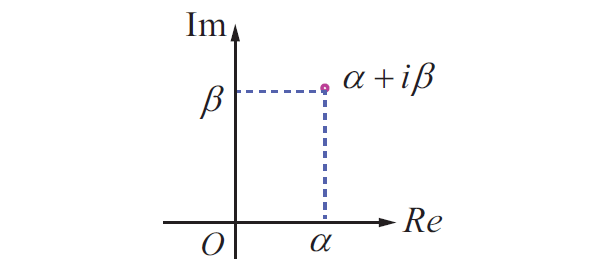PROBABILITY WORKSHEET
Problem 1 :
A coin is tossed three times. Find the probability of getting :
(i) 2 heads
(ii) at least 2 heads
Problem 2 :
A dice is rolled twice. What is the probability of getting a difference of 2 points ?
Problem 3 :
Two dice are thrown simultaneously. Find the probability that the sum of points on the two dice would be 7 or more.
Problem 4 :
What is the chance of picking a spade or an ace not of spade from a pack of 52 cards ?
Problem 5 :
Find the probability that a four digit number comprising the digits 2, 5, 6 and 7 would be divisible by 4.
Problem 6 :
A committee of 7 members is to be formed from a group comprising 8 gentlemen and 5 ladies. What is the probability that the committee would comprise :
(a) 2 ladies,
(b) at least 2 ladies.
Problem 7 :
A strabismus surgery has a probability of 0.9 of success in the first attempt and a probability of 0.98 of success in the second attempt. Use the techniques of tree diagrams to find the probability that the surgery will be successful within two attempts. (round four digits after the decimal).
Problem 8 :
Find the probability that a four digit number comprising the digits 2, 5, 6 and 7 would be divisible by 4.

1. Answer :
When a coin is tossed three times, first we need enumerate all the elementary events.
This can be done using 'Tree diagram' as shown below :

So, the elementary events are HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
That is,
S = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }
Thus, the number of elementary events n(s) = 8.
(i) 2 heads :
Out of these 8 outcomes, 2 heads occur in three cases namely HHT, HTH and THH.
If we denote the occurrence of 2 heads by the event A and if assume that the coin as well as performer of the experiment is unbiased then this assumption ensures that all the eight elementary events are equally likely.
Then by the classical definition of probability, we have
P(A) = n(A)/n(s)
= 3/8
= 0.375 or 37.5%
(ii) at least 2 heads :
Let B denote occurrence of at least 2 heads i.e. 2 heads or 3 heads.
Since 2 heads occur in 3 cases and 3 heads occur in only 1 case, B occurs in 3 + 1 or 4 cases.
By the classical definition of probability,
P(B) = 4/8
= 0.50 or 50%
2. Answer :
If an experiment results in p outcomes and if the experiment is repeated q times, then the total number of outcomes is pq.
In the present case, since a dice results in 6 outcomes and the dice is rolled twice, total no. of outcomes or elementary events is 62 or 36.
We assume that the dice is unbiased which ensures that all these 36 elementary events are equally likely.
Now a difference of 2 points in the uppermost faces of the dice thrown twice can occur in the following cases :
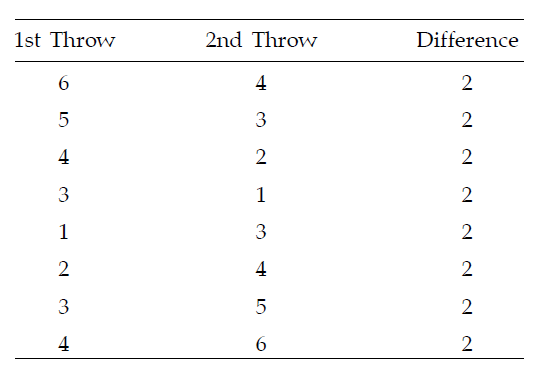
Thus denoting the event of getting a difference of 2 points by A, we find that the no. of outcomes favorable to A, from the above table, is 8.
By classical definition of probability, we get
P(A) = 8/36
= 2/9
3. Answer :
If two dice are thrown then, as explained in the last problem, total no. of elementary events is 62 or 36.
Now a total of 7 or more i.e. 7 or 8 or 9 or 10 or 11 or 12 can occur only in the following combinations :
sum = 7 ----> (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
sum = 8 ----> (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
sum = 9 ----> (3, 6), (4, 5), (5, 4), (6, 3)
sum = 10 ----> ((4, 6), (5, 5), (6, 4)
sum = 11 ----> (5, 6), (6, 5)
sum = 12 ----> (6, 6)
Thus the no. of favorable outcomes is 21. Letting A stand for getting a total of 7 points or more, we have
P(A) = 21/36
= 7/12
4. Answer :
A pack of 52 cards contain 13 Spades, 13 Hearts, 13 Clubs and 13 Diamonds.
Each of these groups of 13 cards has an ace.
Hence the total number of elementary events is 52 out of which 13 + 3 or 16 are favorable to the event A representing picking a Spade or an ace not of Spade.
Thus we have
P(A) = 16/52
= 4/13
5. Answer :
Since there are four digits, all distinct, the total number of four digit numbers that can be formed without any restriction is 4! or 4 × 3 × 2 × 1 or 24.
Now a four digit number would be divisible by 4 if the number formed by the last two digits is divisible by 4.
This could happen when the four digit number ends with 52 or 56 or 72 or 76.
If we fix the last two digits by 52, and then the 1st two places of the four digit number can be filled up using the remaining 2 digits in 2! or 2 ways.
That is,
6752
7652
Thus there are 2 four digit numbers that end with 52.
Proceeding in this manner, we find that the number of four digit numbers that are divisible by 4 is 4 × 2 or 8.
If A denotes the event that any four digit number using the given digits would be divisible by 4, then we have
P(A) = 8/24
= 1/3
6. Answer :
Since there are altogether 8 + 5 or 13 persons, a committee comprising 7 members can be formed in
13C7 = 13C6 = (13x12x11x10x9x8)/(6x5x4x3x2x1)
13C7 = 11x12x13
13C7 = 429
(a) 2 ladies :
When the committee is formed taking 2 ladies out of 5 ladies, the remaining (7–2) or 5 committee members are to be selected from 8 gentlemen.
Now 2 out of 5 ladies can be selected in 5C2 ways and 5 out of 8 gentlemen can be selected in 8C5 ways.
Thus if A denotes the event of having the committee with 2 ladies, then A can occur in 5C2 x 8C5 ways
5C2 x 8C5 = 5C2 x 8C3
5C2 x 8C5 = 10 x 56
5C2 x 8C5 = 560
Hence,
P(A) = 560/1716
= 140/429
(b) at least 2 ladies :
Since the minimum number of ladies is 2, we can have the following combinations :

Thus if B denotes the event of having at least two ladies in the committee, then B can occur in
= (5C2 × 8C5) + (5C3 × 8C4) + (5C4 × 8C3) + (5C5 × 8C2)
= 1568 ways
So,
P(B) = 1568/1716
= 392/429
7. Answer :
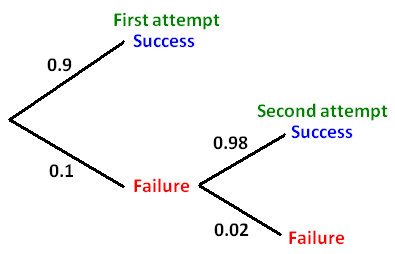
When we go through the question, we have to carefully look at the term "within two attempts".
We are going to get answer for our question from this term.
"Within two attempts" means "less than two attempts".
That is, no. of attempts allowed for success = 0, 1.
We can not get success in 0 attempts. (That is, without any attempt, it is impossible to have success).
To satisfy the condition "within two attempts", possible no. of attempts can be made to get success = 1.
From the the above tree diagram, it is very clear that the probability for success in the first attempt is 0.9.
So, probability that the surgery will be successful within two attempts is 0.9.
8. Answer :
Because there are four digits and all digits are distinct, the total number of four digit numbers that can be formed without any repetition is
= 4!
= 4 x 3 x 2 x 1
= 24
n(S) = 24
Now a four digit number would be divisible by 4, if the number formed by the last two digits is divisible by 4.
This could happen when the four digit number ends with 52 or 56 or 72 or 76.
If we fix the last two digits by 52, and then the first two places of the four digit number can be filled up using the remaining 2 digits in 2! or 2 ways.
That is,
(6752, 7652)
Thus, there are 2 four digit numbers that end with 52.
Proceeding in this manner, we find that the number of four digit numbers that are divisible by 4 as follows.
(2756, 7256)
(5672, 6572)
(2576, 5276)
So, there are are 8 four digit numbers which are divisible by 4.
Let A denote the event that any four digit number using the digits 2, 5, 6 and 7 would be divisible by 7.
Then,
P(A) = n(A)/n(S)
= 8/24
= 1/3
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane