PERIMETER OF PARALLELOGRAM

Perimeter is a path that surrounds a two dimensional shape. The term may be used either for the path or its length it can be thought of as the length of the outline of a shape.

Parallelogram is a quadrilateral in which opposite sides are parallel and equal as shown below. 

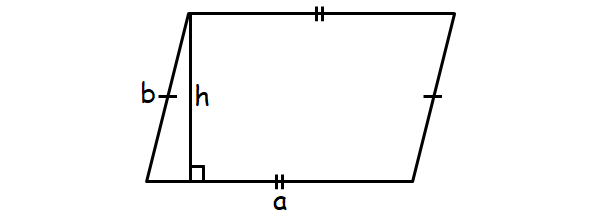
Formula for perimeter of a parallelogram : 

= 2a + 2b

= 2(a + b) units

Example 1 :

Find the perimeter of a parallelogram with the base and side length are 15 cm and 12 cm.

Solution :

Perimeter of a parallelogram :

= 2(a + b)

Substitute a = 15 and b = 12.

= 2(15 + 12)

= 2(27)

= 54 cm

Example 2 :

Find the perimeter of parallelogram with the base and side length are 9 ft and 3 ft.

Solution :

Perimeter of a parallelogram :

= 2(a + b)

Substitute a = 9 and b = 3.

= 2(9 + 3)

= 2(12)

= 24 cm

Example 3 :

If the perimeter of parallelogram is 40 in and its base is 15 in, find its side length.

Solution :

Perimeter of a parallelogram = 40

2(a + b) = 40

Substitute a = 15.

2(15 + b) = 40

30 + 2b = 40

Subtract 30 from each side.

2b = 10

Divide each side by 2.

b = 5

The side length of the parallelogram is 5 in.

Example 4 :

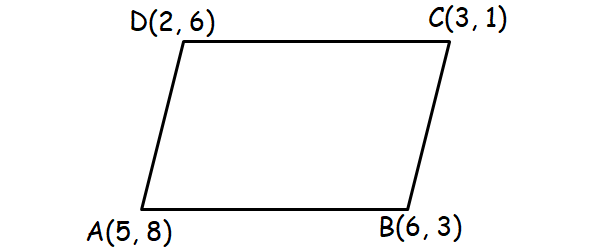
Prove that the points (5, 8), (6, 3), (3, 1) and (2, 6) form a parallelogram and also find the perimeter.

Solution :

Let A(5, 8), B(6, 3), C(3, 1) and D(2, 6).

Formula to find the distance between two points :

d = √[(x₂ - x₁)² + (x₂ - x₁)²]

Length of AB :

Substitute (x₁, y₁) = A(5, 8) and (x₂, y₂) = B(6, 3) in the distance formula.

AB = √[(6 - 5)² + (3 - 8)²]

= √[(1)² + (-5)²]

= √[1 + 25]

= √26

Length of BC :

Substitute (x₁, y₁) = B(6, 3) and (x₂, y₂) = C(3, 1) in the distance formula.

BC = √[(3 - 6)² + (1 - 3)²]

= √[(-3)² + (-2)²]

= √[9 + 4]

= = √13

Length of DC :

Substitute (x₁, y₁) = D(2, 6) and (x₂, y₂) = C(3, 1) in the distance formula.

DC = √[(3 - 2)² + (1 - 6)²]

= √[(1)² + (-5)²]

= √[1 + 25]

= = √26

Length of AD :

Substitute (x₁, y₁) = A(5, 8) and (x₂, y₂) = D(2, 6) in the distance formula.

AD = √[(2 - 5)² + (6 - 8)²]

= √[(-3)² + (-2)²]

= √[9 + 4]

= = √13

length of AB = length of DC

length of AD = length of BC

Opposite sides are equal. So, the given points form a parallelogram.

Perimeter = 2(√26 + √13) units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.