HOW TO SHOW TWO CIRCLES ARE ORTHOGONAL
Two circles are said to be orthogonal circles, if the tangent at their point of intersection are at right angles.
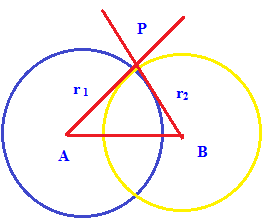
If two circles are cut orthogonally then it must satisfy the following condition.
2 g1 g2 + 2 f1 f2 = c1 + c2
General equation of circle :
x2 + y2 + 2gx + 2fy + c = 0
Example 1 :
Show that the circles
x2 + y2 - 8x + 6y - 23 = 0
and
x2 + y2 - 2x - 5y + 16 = 0
are orthogonal.
Solution :
From 1st equation :
x2 + y2 - 8x + 6y - 23 = 0
x2 + y2 + 2g1x + 2f1y + c1 = 0
2g1 = -8, g1 = -4
2f1 = 6, f1 = 3
and c1 = -2
From 2nd equation :
x2 + y2 - 2x - 5y + 16 = 0
2g2 = -2, g2 = -1
2f2 = -5, f2 = -5/2
and c2 = 16
Condition to prove two circles are orthogonal :
2 g1 g2 + 2 f1 f2 = c1 + c2
2(-4)(-1)+2(3)(-5/2) = -23+16
8-15 = -7
- 7 = -7
The two circles cut orthogonally and hence they are orthogonal circles.
Example 2 :
Show that the circles
x2 + y2 - 8x + 6y + 21 = 0
and
x2 + y2 - 2y - 15 = 0
are orthogonal.
Solution :
From 1st equation :
x2 + y2 - 8x + 6y + 21 = 0
x2 + y2 + 2g1x + 2f1y + c1 = 0
2g1 = -8, g1 = -4
2f1 = 6, f1 = 3
and c1 = 21
From 2nd equation :
x2 + y2 - 2y - 15 = 0
x2 + y2 + 2g2x + 2f2y + c2 = 0
2g1 = 0, g1 = 0
2f1 = -2, f1 = -1
and c1 = -15
2 (-4) (0) + 2 (-3) (-1) = 21 - 15
Condition to prove two circles are orthogonal :
2 g1 g2 + 2 f1 f2 = c1 + c2
2(-4)(0)+2(-3)(-1) = 21-15
0+6 = 6
6 = 6
The two circles cut orthogonally and hence they are orthogonal circles.
Example 3 :
Find the equation of the circle which passes through the point (1, 2) and cuts orthogonally each of the circles
x2 + y2 = 9
and
x2 + y2 − 2x + 8y − 7 = 0
Solution :
Let the required equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ------(1)
The point (1, 2) lies on the circle
1+4+2g+4f+c = 0
2g+4f+c = −5 -----(2)
The circle (1) cuts the circle x2 + y2 = 9 orthogonally.
2g1g2 + 2f1f2 = c1 + c2
2g(0) + 2f(0) = c − 9
c = 9 ---(3)
Again the circle (1) cuts
x2 + y2 − 2x + 8y − 7 = 0
orthogonally.
2g(− 1) + 2f(4) = c − 7
-2g + 8f = 9 − 7 = 2
−g + 4f = 1 -----(4)
(2) becomes 2g + 4f = − 14
g + 2f = − 7 ------(5)
(4) + (5) => 6f = − 6 ⇒ f = − 1
(5) => g − 2 = − 7 => g = − 5
The required equation of the circle is
x2 + y2 − 10x − 2y + 9 = 0

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number -
Conjugate of a Complex Number
Apr 15, 24 11:17 PM
Conjugate of a Complex Number -
Complex Plane
Apr 14, 24 07:56 AM
Complex Plane