ORDER OF OPERATIONS

In the flag shown below, assume there are about 1500 plants in each of the 50 stars of the flag. And also, assume that there are 64000 plants in each of the 7 short stripes and 105000 plants in each of the 6 long stripes. The blue region contains about 200000.

We can approximate the total number of plants by evaluating the following expression :

50 ⋅ 1500 + 7 ⋅ 64000 + 6 ⋅ 105000 + 200000

To evaluate expressions involving more than one operation, mathematicians have agreed on a set of rules called the order of operations.

Order of Operations

1. Evaluate expressions inside grouping symbols.

2. Evaluate powers.

3. Multiply and divide from left to right.

4. Add and subtract from left to right.

Video Lesson

Using Order of Operations

Example 1 :

To approximate the total number of plants described above, use the order of operations to evaluate the expression :

50 ⋅ 1500 + 7 ⋅ 64000 + 6 ⋅ 105000 + 200000

Solution :

= 50 ⋅ 1500 + 7 ⋅ 64000 + 6 ⋅ 105000 + 200000

Multiply.

= 75,000 + 448,000 + 630,000 + 200,000

Add.

= 1,353,000

There are approximately 1,353,000 plants in the flag.

Using Grouping Symbols

Example 2 :

Evaluate the expression :

9(16 - 3.2)

Solution :

= 9(16 - 3.2)

Subtract within parentheses.

= 9(12.8)

Multiply.

= 115.2

Example 3 :

Evaluate the expression :

2.5(16 ÷ 4)

Solution :

= 2.5(16 ÷ 4)

Divide within parentheses.

= 2.5(4)

Multiply.

= 10

Example 4 :

Evaluate the expression :

(18 + 2)/(13 - 8)

Solution :

= (18 + 2)/(13 - 8)

Rewrite fraction as division.

= (18 + 2) ÷ (13 - 8)

Evaluate within parentheses.

= 20 ÷ 5

Divide.

= 4

Example 5 :

Evaluate the expression :

4 ⋅ [38 - (15 + 7)]

Solution :

= 4 ⋅ [38 - (15 + 7)]

Add within parentheses.

= 4 ⋅ [38 - 22]

Subtract within brackets.

= 4 ⋅ 16

Multiply.

= 64

Example 6 :

Evaluate the expression :

[(45 - 3) ÷ (3² + 5)] ⋅ 2 - 5

Solution :

= [(45 - 3) ÷ (3² + 5)] ⋅ 2 - 5

Evaluate within parentheses.

= [42 ÷ (9 + 5)] ⋅ 2 - 5

= [42 ÷ 14] ⋅ 2 - 5

Divide within brackets.

= 3 ⋅ 2 - 5

Multiply.

= 6 - 5

Subtract.

= 1

Evaluating Variable Expressions

Example 7 :

Evaluate the following expression when x = 3 and y = 4.

5(x + y)

Solution :

= 5(x + y)

Substitute 3 for x and 4 for y.

= 5(3 + 4)

Add within parentheses.

= 5(7)

Multiply.

= 35

Example 8 :

Evaluate the following expression when x = 4 and y = 6.

7(x + y)²

Solution :

= 7(x + y)²

Substitute 4 for x and 6 for y.

= 7(4 + 6)²

Add within parentheses.

= 7(10)²

Evaluate power.

= 7(100)

Multiply.

= 700

Example 9 :

Evaluate the following expression when a = 2 and b = 3.

2(a² + b³)

Solution :

= 2(a² + b³)

Substitute 2 for a and 6 for.

= 2(2² + 3³)

Evaluate within parentheses.

= 2(4 + 27)²

Add within parentheses.

= 2 ⋅ 31²

Evaluate power.

= 2 ⋅ 961

= 1922

Problem 10 :

Evaluate :

a³ - (b² - c) ÷ a + (ab - c)

if a = 3, b = 5 and c = 7.

Solution :

= a³ - (b² - c) ÷ a + (ab - c)

Substitute a = 3, b = 5 and c = 7.

= 3³ - (5² - 7) ÷ 3 + (3 ⋅ 5 - 7)

Evaluate within parentheses.

= 3³ - (25 - 7) ÷ 3 + (15 - 7)

= 3³ - 18 ÷ 3 + 8

Evaluate power.

= 27 - 18 ÷ 3 + 8

Divide.

= 27 - 6 + 8

= 21 + 8

= 29

Using a Problem Solving Plan 

Example 11 :

A pattern and enough material are bought to make two pillows. The pattern costs $6. Each pillow requires $4.25 worth of fabric and a button that costs $0.80. Find the total cost.

Solution :

Read and Understand :

One pattern plus fabric and buttons are bought to make pillows. You have to find the total cost.

Make a Plan :

Write a verbal model.

Solve the Problem :

Write and evaluate the expression.

Substitute values into verbal model.

Total cost :

= 6 + 2(4.25 + 0.80)

= 6 + 2(5.05)

= 6 + 10.10

= 16.10

The total cost is $16.10.

Look Back :

Use estimation to check that the answer is reasonable.  The cost of material for each pillow is about

$4 + $1 = $5

The total cost is about

$6 + 2($5) = $16

The answer is reasonable.

Practice Questions

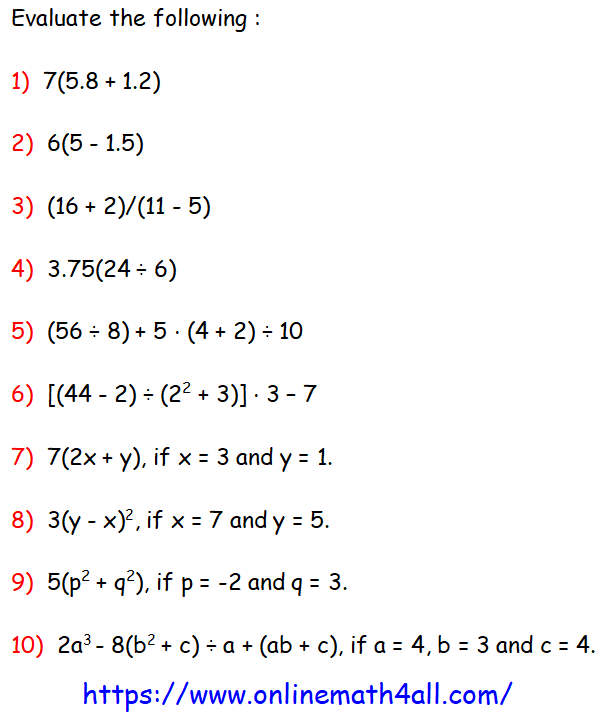
Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.