NEGATIVE EXPONENTS

Consider the following exponential form.

a^-b

Here the base is 'a' and the exponent is '-b'.

To evaluate a^-b, first we have to change the negative sign of the exponent as positive shown below. 

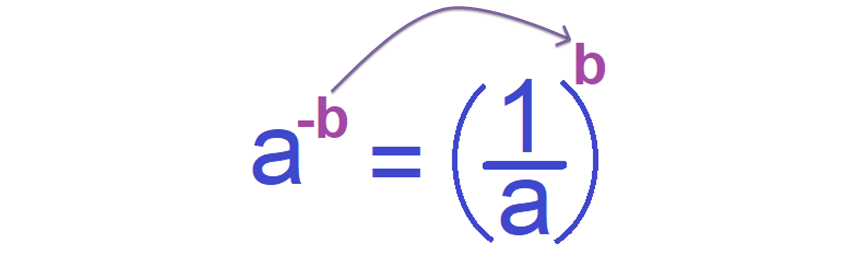
Consider the following exponential form where the base is a fraction.

(a/b)^-m

Here, the negative exponent can be changed positive as shown below.

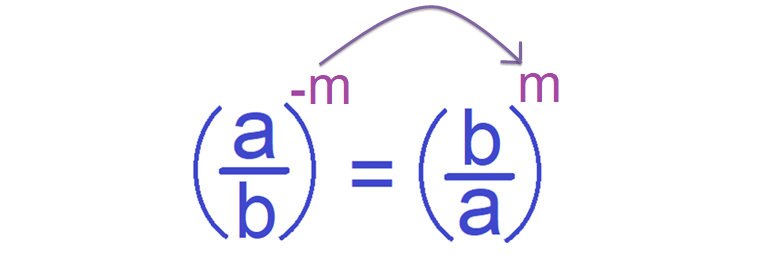
From the above two examples, it is clear that if there is a negative exponent for a base, the negative exponent can be changed as positive exponent by taking the reciprocal to the base.   

Solved Problems

Problem 1 : 

Evaluate : 

8^-2

Solution : 

=  8^-2

=  (1/8)²

Distribute the exponent to numerator and denominator. 

=  1² / 8²

=  1/64

Problem 2 : 

Evaluate : 

(3/2)^-3

Solution : 

=  (3/2)^-3

=  (2/3)³

Distribute the exponent to numerator and denominator. 

=  2³ / 3³

=  8/27

Problem 3 : 

Evaluate : 

(-5/4)^-2

Solution : 

=  (-5/4)^-2

=  (-4/5)²

Since the exponent is even, the negative sign inside the parentheses will become positive. 

=  (4/5)²

Distribute the exponent to numerator and denominator. 

=  4² / 5²

=  16/25

Problem 4 : 

Evaluate : 

(-7/6)^-3

Solution : 

=  (-6/7)^-3

=  (-6/7)³

Since the exponent is odd, the negative sign inside the parentheses will remain same. 

Distribute the exponent to numerator and denominator. 

=  - 6³ / 7³

=  - 216/343

Problem 5 : 

Evaluate : 

(5^-2) ⋅ (3^-4)

Solution : 

=  (5^-2) ⋅ (3^-4)

=  (1/5)² ⋅ (1/3)⁴

=  (1/25) ⋅ (1/81)

=  1/2025

Problem 6 : 

Evaluate : 

3^-4/ 2^-3

Solution : 

=  3^-4/ 2^-3

=  (1/3)⁴/ (1/2)³

=  (1/81) / (1/8)

=  (1/81) ⋅ (8/1)

=  8/81

Problem 7 :

It is given that a^-1/3  =  4/3. Find the value of a. 

Solution : 

a^-1/3  =  4/3

a  =  (4/3)^-3/1

a  =  (4/3)^-3

a  =  (3/4)³

Distribute the exponent to numerator and denominator. 

a  =  3³ / 4³

a  =  27/64

Problem 8 :

It is given that (a/b)^-x  =  (b/a)³. Find the value of x. 

Solution : 

(a/b)^-x  =  (b/a)³

(b/a)^x  =  (b/a)³

x  =  3

Apart from the stuff given above, If you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.