HOW TO MULTIPLY MATRICES
The product of matrix AB is determined by multiplying every row matrix of A by the column matrix of B.
If A = [aij]mxn and B = [bij]nxp then the product matrix AB is defined by
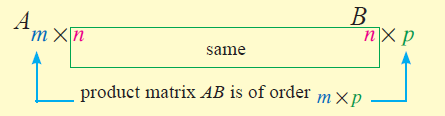
Multiplying Row Matrix by Column Matrix
Question 1 :
Find the product of the matrices, if exists.

Solution :

Order of matrix A is 1 x 2 and order of matrix B is 2 x 1.
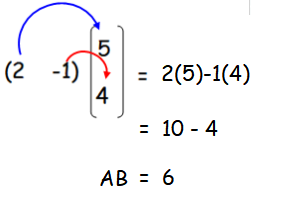
The order of matrix AB is 1 x 1.
Multiplying a Column Matrix by Row Matrix
Question 2 :

then find AB.
Solution :
Order of matrix A is 3 x 1.
Order of matrix B is 1 x 3
Order of matrix AB is 3 x 3.


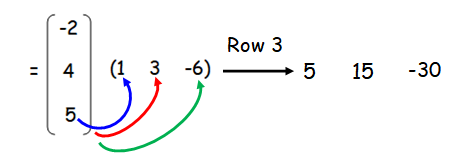
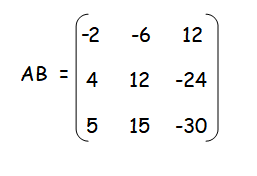
Multiplying Matrices of Different Dimensions
Question 3 :
Find the product of the given matrices.

Solution :
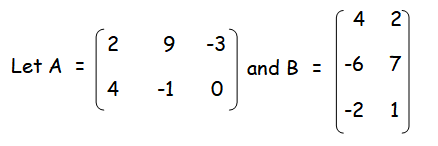
By multiplying the first row of matrix A by the columns of matrix B, we get row 1 of resultant matrix AB.
By multiplying the second row of matrix A by the columns of matrix B, we get row 2 of resultant matrix AB.
Order of matrix A is 2 x 3, order of matrix B is 3 x 2.
So, the order of matrix AB will be 2 x 2.
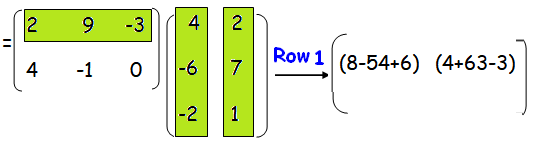
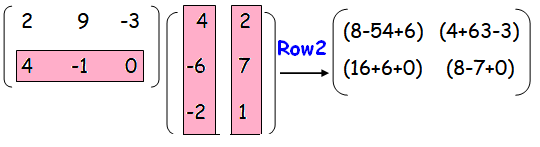
By doing simplification, we get the result.


Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Factoring Quadratic Trinomials Worksheet
Apr 25, 24 07:47 PM
Factoring Quadratic Trinomials Worksheet -
Factoring Quadratic Trinomials
Apr 25, 24 07:03 PM
Factoring Quadratic Trinomials - Methods - Solved Examples -
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems


