MATH TERMS THAT START WITH L
Laplace Transform :
Laplace transform is an integral transform widely used in math, with many applications of physics and engineering.
Lateral Area :
Lateral area is the surface area of a three dimensional objects excluding their bases.
Least Common Denominator :
The least common multiple of the denominators of the fraction is called as least common denominator. For example 6 is the least common denominator for the fractions 1/2 and 2/3.
Least Common Multiple :
LCM is the least multiple of common multiples of two numbers.
Example :
Find the LCM for 5 and 6.
To find the LCM first we have to find the multiples of 5 and 6.
Multiples of 5 = {5, 10, 15, 20, 25, 30, 35, ....}
Multiples of 6 = {6, 12, 18, 24, 30, 36, ....}
LCM of 5 and 6 = 30
Like Terms :
Like terms are terms that contain the same variables raised to the same power. While doing addition or subtraction we have to combine the like terms together and do the operation.
For example,
x3y and 4x3y are like terms
Linear Equation :
In linear equation the highest power of the variables x and y always be 1 .So if we graph this equation we will get the line in the graph. The general form of any linear equation is ax + by + c = 0.
Line :
A set of points that extend infinitely in opposite directions is called line. We use the symbol. The line has many points.

Line Segment :
A line which has two end points is called line segment.

Logarithms :
Logarithms were invented independently by John Napier(in 1614) and Joost Burgi (in 1620). Log is being useful in many fields from astronomy to common finance.
Lagrange Theorem :
We know multiplication is helpful shortcut for addition, and the topic exponent is one of the short cut for multiplication, and log is the short cut for exponents.
If f (x) be a real valued function that satisfies the following conditions.
1) f(x) is defined and continuous on the closed interval [a, b].
2) f(x) is differentiable on the open interval (a, b).
Then there exists at least one point c ∊ (a,b) such that
f'(c) = [f(b) - f(a)] / (b - a)
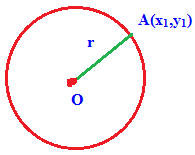
Locus :
Generally locus of the point can be defined as the path traced by a point when it is moving with a specific geometrical conditions.
In the diagram below the point A(x1, y1) which lies on the circle whose distance from the point O(h, k) is a constant r.
The fixed point O is called the center of the circle and the distance from O to A is called radius r.
Least Integer Function :
The function whose value at any real number x is the smallest integer greater than or equal to x is called the least integer function and it is denoted by ⌈x⌉.
L' Hopital Rule :
Let f and g be continuous real valued functions defined on the closed interval [a, b].
f, g be differentiable on (a, b) and g'(c) ≠ 0.
Then if
lim x-> c f(x) = 0
lim x-> c g(x) = 0 and
if lim x-> c f'(c)/g'(c) = L
Limit :
Let f be a function of real variable x. Let c, l be two fixed numbers. If f(x) approaches the value l as x approaches c, we can say l is the limit of the function f (x) as tends to c. This can be written as lim x ->c f(x) = L.
Left Hand Limit :
X tends to c from below or from the left and write it symbolically as x -> c-0 or simply x -> c- .
The limit of f with this restriction on x is called the left hand limit.
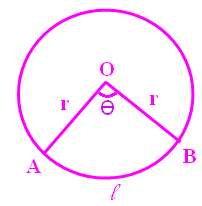
Length of Arc :
In a sector with central angle AOB = θ and radius r. The length of AB is called length of arc.
Length of arc = (θ/360) ⋅ 2Πr
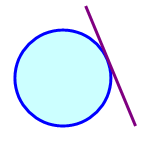
Length of Tangent :
In this page we are going to see how to find the length of the tangent to the circle from the point (x1, y1).
Length of the tangent = √(x12+y12+2gx1+2fy1+c)
Laws of Set Operations :
Some Laws on set operations are discussed here :
Identity laws :
A∪∅ = A
A∩U = U
Domination laws :
A∪U = U
A∩∅ = ∅
Idempotent Laws :
A∪A = A
A∩A = A
Commutative laws :
A∪B = B∪A
A∩B = B∩A
Leading Coefficients :
The coefficient of leading polynomial is called leading coefficient.
Let us consider the expression,
2x3+5x2+3
In this polynomial the leading term is 2x³ and the coefficient is of this is 2.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems -
Converting Between Polar and Rectangular Coordinates
Apr 23, 24 11:08 AM
Converting Between Polar and Rectangular Coordinates
