SOLVING LINEAR EQUATIONS IN 2 VARAIBLES USING INVERSION METHOD
Formula for inversion method :
X = A⁻¹ B
Example 1 :
Solve the following linear equation by inversion method
x + y = 3, 2x + 3y = 8
Solution :
First we have to write the given equation in the form
AX = B
Here X represents the unknown variables. A represent coefficient of the variables and B represents constants.
|
|
|
To solve this we have to apply the formula
X = A⁻¹ B
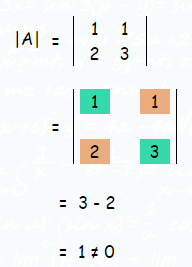
Since A is a non singular matrix. A⁻¹ exists.
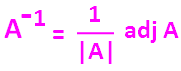
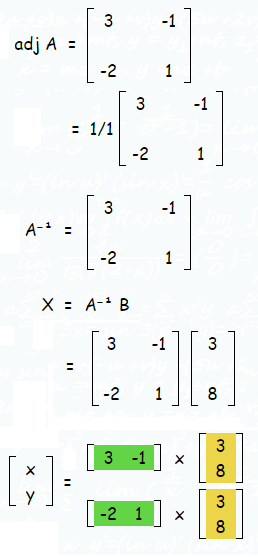
|
x = 9 - 8 x = 1 |
y = -6 + 8 y = 2 |
Example 2 :
Solve the following linear equation by inversion method
2x - y = 7, 3x - 2y = 11
Solution :
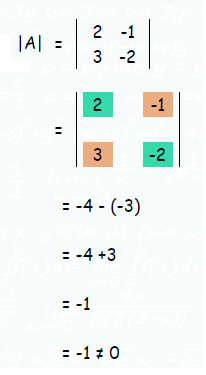
To solve this we have to apply the formula X = A⁻¹ B
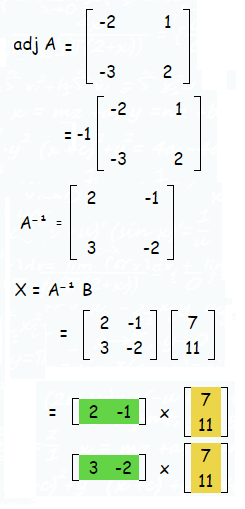
|
x = 14 - 11 x = 3 |
y = 21 - 22 y = -1 |

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
2. Matrix Inverse Calculator - 2x2 Matrix
3. Matrix Inverse Calculator - 3x3 Matrix
4. Matrix Inverse Calculator - 4x4 Matrix
5. Cramer's Rule Calculator - 3x3 Matrix
6. Matrix Addition Calculator - 3x3 Matrix
7. Matrix Subtraction Calculator - 3x3 Matrix
8. Matrix Multiplication Calculator - 2x2 Matrix
9. Matrix Multiplication Calculator - 3x3 Matrix
10. Matrix Determinant Calculator - 3x3 & 2x2 Matrix
11. Matrix Addition Calculator - 2x2 Matrix
12. Matrix Subtraction Calculator- 2x2 Matrix
13. Matrix Addition Calculator - 4x4 Matrix
14. Matrix Subtraction Calculator- 4x4 Matrix
15. Matrix Multiplication Calculator - 4x4 Matrix