INVERSE FUNCTION
Let f be a one-one onto function from A to B.
Let y be an arbitrary element of B.
Then f being onto, there exists an element x in A such that
f(x) = y
So, we may define a function, denoted as f-1 as
f-1 : B ---> A : f-1(y) = x
if and only if f(x) = y.
The above function f-1 is called the inverse of f.
A function is invertible, if and only if f is one-one onto.
More clearly, one-one onto function will have an inverse function
You may be able to find f-1 for any function f.
But, f-1 will also be a function, only if f is one-one onto function.
Remarks :
If f is one-one onto, then f-1 is also one-one onto.
Illustration :
If f : A ---> B, then
f-1 : B---> A
How to find inverse of a function f(x) :
Step 1 :
Replace f(x) by y.
Step 2 :
Interchange the variables x and y.
Step 3 :
Solve for y.
Step 4 :
Replace y by f-1(x).
Example 1 :
Find the inverse of the function f(x) = 2x + 3.
Solution :
f(x) = 2x + 3
Replace f(x) by y.
y = 2x + 3
Interchange x and y.
x = 2y + 3
Solve for y.
x - 3 = 2y
y = (x - 3)/2
Replace y by f-1(x).
f-1(x) = (x - 3)/2
f-1 (x) = (x - 3)/2
Example 2 :
Find the inverse of the function f(x) = x2.
Solution :
Replace f(x) by y.
y = x2
Interchange x and y.
x = y2
y2 = x
Solve for y. Taking square root on both sides,
y = ±√x
Replace y by f-1(x).
f-1(x) = ±√x
Example 3 :
Find the inverse of the function h(x) = log10(x).
Solution :
h(x) = log10(x)
Replace h(x) by y.
y = log10(x)
Interchange x and y.
x = log10(y)
Solve for y.
y = 10x
Replace y by h-1(x).
h-1(x) = 10x
Example 4 :
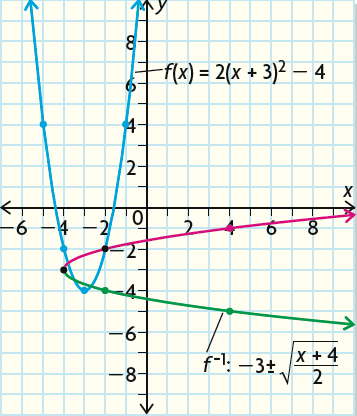
Find the inverse of the quadratic function and graph it.
f(x) = 2(x + 3)2 - 4
Solution :
Replace f(x) by y.
y = 2(x + 3)2 - 4
Interchange x and y.
x = 2(y + 3)2 - 4
Solve for y.
x + 4 = 2(y + 3)2
(x + 4)/2 = (y + 3)2
Take square root on both sides.
±√[(x + 4)/2] = y + 3
±√[(x + 4)/2] - 3 = y
y = -3 ± √[(x + 4)/2]
Replace y by f-1(x).
f-1(x) = -3 ± √[(x + 4)/2]
Graphing the inverse of f(x) :
We can graph the original function by plotting the vertex (-3, -4). The parabola opens up, because a is positive.
And we get f(-2) = -2 and f(-1) = 4, which are also the same values of f(-4) and f(-5) respectively.
To graph f-1(x), we have to take the coordinates of each point on the original graph and switch the x and y coordinates.
For example, (-1, 4) becomes (4, -1).
We have to do this because the input value becomes the output value in the inverse, and vice versa.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems
