FINDING INVERSE OF A MATRIX USING FORMULA

What is inverse of a matrix ?

For a square matrix A, the inverse is written A^-1. When A is multiplied by A^-1 the result is the identity matrix I. Non square matrices do not have inverses.

Note: Not all square matrices have inverses. A square matrix which has an inverse is called invertible or nonsingular, and a square matrix without an inverse is called non invertiable or singular.

Formula to find the inverse of the matrix :

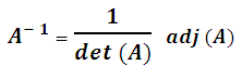
Example 1 :

Find the inverse of the following matrix

Solution :

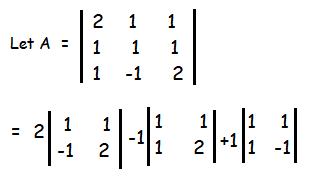
|A|  =  2(2+1) - 1(2-1) + 1(-1-1)

|A|  =  2(3) - 1(1) + 1(-2)

|A|  =  6-1-2

|A|  =  3  ≠ 0

Since A is a non singular matrix. A^-1 exists.

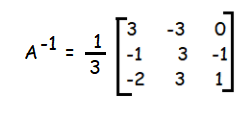
Example 2 :

Find the inverse of the following matrix

Solution :

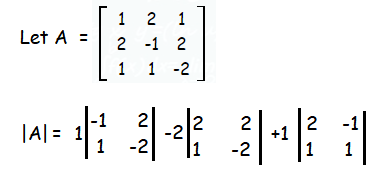
|A|  =  1(2-2)-2(-4-2)+1(2+1)

  =  1(0) - 2(-6)+1(3)

  =  12 + 3

|A|  =  15  ≠ 0

Since A is a non singular matrix. A^-1 exists.

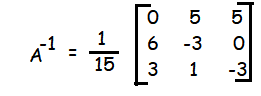
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.