INTEGRATION WORKSHEET WITH SOLUTONS
Integrate the following with respect to x
(1) 5x4+3(2x+3)4-6(4-3x)5
(2) (3/x)+[m/(4x+1)]-2(5-2x)5
(3) 4 - 5/(x+2) + 3 cos 2x
(4) 3e7x-4sec(4x+3)tan(4x+3)+11/x5
(5) pcosec2(px-q)-6(1-x)4+4e(3-4x)
(6) (2x-5) (36+4x)
(7) (1 + x3)2
(8) (x3+4x2-3x+2)/x2
(9) (x4 - x2 + 2)/(x + 1)
(10) (1+x)2/√x

Question 1 :
5x4+3(2x+3)4-6(4-3x)5
Solution:
Now we are going to integrate the given function
= ∫[5x4+3(2x+3)4-6(4-3x)5] dx
= ∫5x4 dx + 3∫(2x+3)4 dx - 6∫(4-3x)5 dx
= x5 dx + (3/10)(2x+3)5 + (1/3)(4-3x)6 dx
Question 2 :
(3/x)+[m/(4x+1)]-2(5-2x)5
Solution :
Now we are going to integrate the given function
= ∫(3/x)+[m/(4x+1)]-2(5-2x)5 dx
= 3∫(1/x) dx + m∫[1/(4x+1)] dx - 2∫(5-2x)5 dx
= 3log x+(m/4) log (4x+1)+(1/6)(5-2x)6+C
Question 3 :
4 - 5/(x+2) + 3 cos 2x
Solution :
Now we are going to integrate the given function
= ∫(4 - 5/(x + 2) + 3 cos 2x) dx
= 4∫dx - 5∫[1/(x+2)] dx + 3∫cos 2 x dx
= 4x-5 log (x+2) + (3/2) sin 2x + C
Question 4 :
3e7x-4sec(4x+3)tan(4x+3)+11/x5
Solution :
Now we are going to integrate the given function
= ∫(3e7x-4sec(4x+3)tan(4x+3)+11/x5) dx
= 3∫e7x dx - 4∫sec(4x+3)tan(4x+3) dx + 11∫x-5 dx
= (3/7) e7x - sec (4x+3) - (11/4x4) + C
Question 5 :
pcosec2(px-q)-6(1-x)4+4e(3-4x)
Solution :
Now we are going to integrate the given function
= ∫[pcosec2(px-q)-6(1-x)4+4e(3-4x) ] dx
= p∫cosec2 (px-q) dx - 6∫(1-x)4 dx + 4 ∫e(3-4x) dx
= -cot (px-q)- (6/5)(1-x)5 -e(3-4x) + C
Question 6 :
(2x-5) (36+4x)
Solution :
= ∫(2x-5) (36+4x) dx
= ∫[2x(36) + 2x(4x) - 5(36) - 5(4x)] dx
= ∫[52x+8x2-180] dx
= ∫52 x dx + ∫8x2 dx - ∫180 dx
= 52 ∫ x dx + 8 ∫ x² dx - 180 ∫ dx
= 52x2/2 + 8x3/3 - 180x + C
= 26x2 + 8x3/3 - 180x + C
Question 7 :
(1 + x3)2
Solution :
(a+b)2 = a2+2ab+b2
= ∫(1+x3)2 dx
= ∫(1+2x3+x6) dx
= ∫1 dx + ∫2x3 dx + ∫x6 dx
= x+2∫x3dx + ∫x6 dx
= x+2x4/4 + x7/7 + C
= x+x4/2+x7/7+C
= ( x7/7) + (x4/2) + x + C
Question 8 :
(x3+4x2-3x+2)/x2
Solution :
= ∫[(x3+4x2-3x+2)/x2] dx
= ∫x dx + ∫4 dx - ∫(3/x) dx + ∫(2/x2) dx
= x2/2 + 4 x - 3 log x - 2/x + C
Question 9 :
(x4 - x2 + 2)/(x + 1)
Solution :
Now we are going to integrate the given function
= ∫ (x4-x2+2)/(x+1) dx
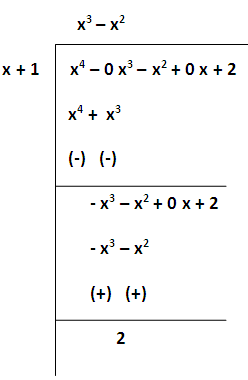
= ∫ [(x3-x2) + 2/(x+1)] dx
= ∫(x3-x2) dx + ∫ 2/(x+1) dx
= (x4/4) - (x3/3) + 2 log (x + 1) + C
Question 10 :
(1+x)2/√x
Solution :
= ∫[(1+x)2/√x] dx
(a + b)2 = a2+2ab+b2
= ∫[(1+2x+x2)/√x] dx
= ∫[(1/√x) dx + ∫(2x/√x) dx + ∫ x2/√x dx
= 2√x + 2 (2/3) x √x + (2/5) x2√x + C
= 2√x + (4/3) x √x + (2/5) x2√x + C

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Multi Step Algebra Word Problems
Apr 23, 24 09:10 PM
Multi Step Algebra Word Problems -
Solving Multi Step Word Problems Worksheet
Apr 23, 24 12:32 PM
Solving Multi Step Word Problems Worksheet -
Solving Multi Step Word Problems
Apr 23, 24 12:07 PM
Solving Multi Step Word Problems