INCENTER OF A TRIANGLE

The internal bisectors of the three vertical angle of a triangle are concurrent. This point of concurrency is called the incenter of the triangle. The incenter is deonoted by I.

How to Find the Coordinates of the Incenter of a Triangle

Let ABC be a triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃).

Let AD, BE and CF be the internal bisectors of the angles of the ΔABC.

The incentre I of ΔABC is the point of intersection of AD, BE and CF.

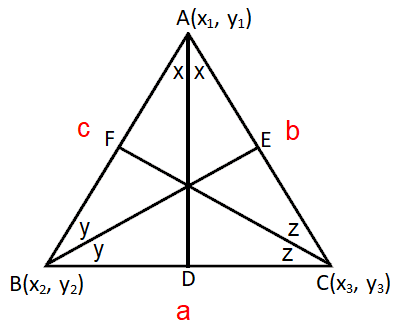
Let 'a' be the length of the side opposite to the vertex A, 'b' be the length of the side opposite to the vertex B and 'c' be the length of the side opposite to the vertex C. 

That is,

AB  =  c, BC  =  a and CA  =  b

Then the formula given below can be used to find the incenter I of the triangle is given by

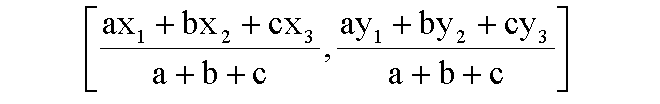
Example : 

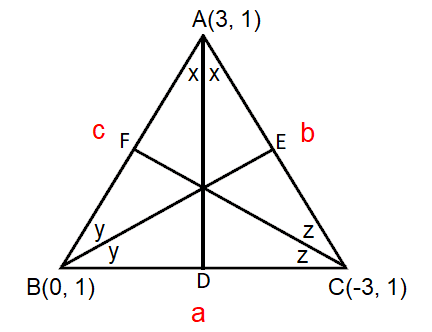
Find the coordinates of the incenter of the triangle whose vertices are A(3, 1), B(0, 1) and C(-3, 1).

Solution :

The vertices of the triangle are

A(3, 1), B(0, 1) and C(-3, 1)

Let 'a' be the length of the side opposite to the vertex A, 'b' be the length of the side opposite to the vertex B and 'c' be the length of the side opposite to the vertex C. 

That is,

AB  =  c, BC  =  a and CA  =  b

Use distance formula to find the values of 'a', 'b' and 'c'.

a  =  BC  =  √[(0+3)² + (1-1)²]  =  √9  =  3

b  =  AC  =  √[(3+3)² + (1-1)²]  =  √36  =  6

c  =  AB  =  √[(3-0)² + (1-1)²]  =  √9  =  3

Incenter I, of the triangle is given by

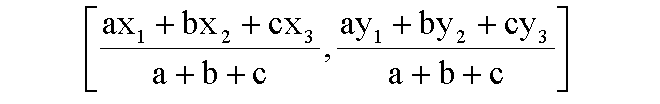
Here, 

(x₁, y₁)  =  (3, 1)

(x₂, y₂)  =  (0, 1)

(x₃, y₃)  =  (-3, 1)

a  =  3, b  =  6 and c  =  3

Then, 

ax₁ + bx₂ + cx₃  =  3(3) + 6(0) + 3(-3)  =  0

ay₁ + by₂ + cy₃  =  3(1) + 6(1) + 3(1)  =  12   

a + b + c  =  3 + 6 + 3  =  12

Substitute the above values in the formula. 

Incenter is

=  (0/12, 12/12)

=  (0, 1)

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.